|
Второй закон Ньютона
|
||||||
|
Второй закон Ньютона устанавливает связь между силой
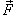 , действующей на тело массы m, и ускорением , действующей на тело массы m, и ускорением 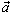 , которое приобретает тело под действием этой силы. , которое приобретает тело под действием этой силы.Ускорение тела 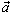 прямо пропорционально действующей силе прямо пропорционально действующей силе 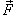 и обратно пропорционально массе тела m, то есть и обратно пропорционально массе тела m, то есть
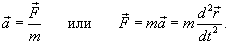 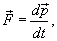 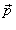 − импульс (количество движения) тела. − импульс (количество движения) тела.В общем случае сила 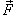 зависит от координат тела, т.е. радиус-вектора зависит от координат тела, т.е. радиус-вектора 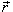 , его скорости , его скорости 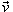 и времени t: и времени t:
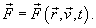 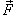 зависит лишь от одной из указанных переменных. зависит лишь от одной из указанных переменных.
Сила зависит от времени: F = F(t)
В предположении, что движение одномерное, второй закон Ньютона в этом случае записывается в виде дифференциального уравнения второго порядка:
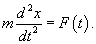 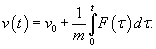 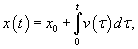
Сила зависит от скорости: F = F(v)
При движении твердого тела в жидкой или газообразной среде на него действует сила сопротивления (или вязкого трения). При малых скоростях 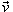 эта сила пропорциональна скорости эта сила пропорциональна скорости 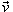 : :
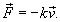 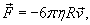 При таком режиме движения второй закон Ньютона записывается (в одномерном приближении) в виде следующего дифференциального уравнения: 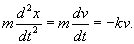 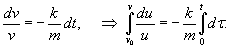 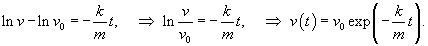 Закон движения 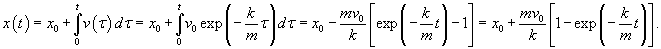 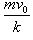 , т.е. пропорционален начальному импульсу тела mv0. , т.е. пропорционален начальному импульсу тела mv0.При увеличении скорости движения тела физика процесса изменяется. Кинетическая энергия тела начинает расходоваться не только на трение между слоями жидкости, но и на перемещение объема жидкости впереди тела. В этом режиме сила сопротивления становится пропорциональной квадрату скорости: 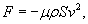 Описанный нелинейный режим возникает при условии 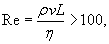 Рассматривая одномерное движение, запишем второй закон Ньютона для этого случая в виде 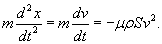 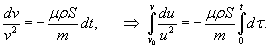 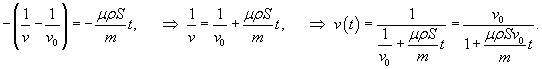 
Сила зависит от координаты: F = F(x)
Примерами сил, зависящих лишь от координаты, является, в частности:
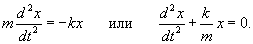 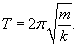 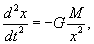 Решение этого уравнения приводится на странице Закон всемирного тяготения. В случае, когда сила зависит от координаты, ускорение удобно представить в таком виде: 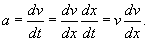 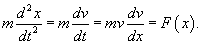 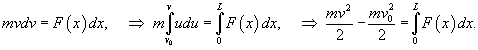 Последующее интегрирование функции v(t) позволяет найти закон движения тела x(t). К сожалению, это не всегда можно сделать аналитически из-за громоздкости выражения для v(t). |
||||||
|
Пример 1
|
||||||
|
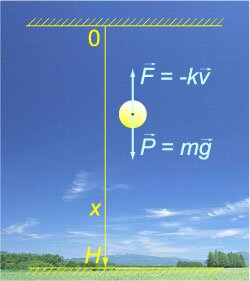
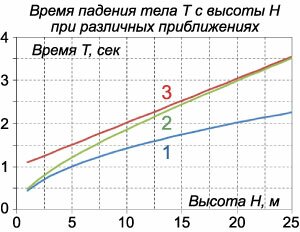
Тело начинает падать с высоты H под действием силы тяжести. В процессе падения оно испытывает сопротивление, пропорциональное скорости. Определить время падения.
Решение.
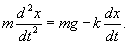 Сначала определим закон изменения скорости v(t) из уравнения 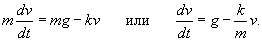 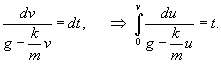 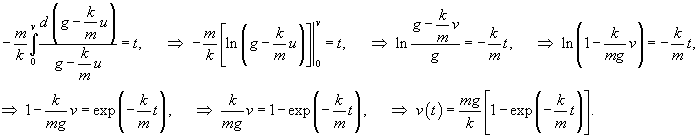 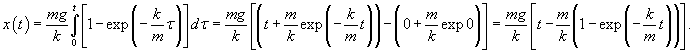 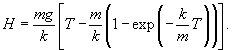 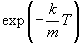 стремится к нулю при больших T. Тогда стремится к нулю при больших T. Тогда

|
||||||
|
Пример 2
|
||||||
|
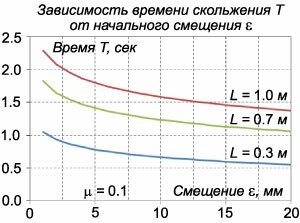
В начальный момент цепочка длиной L свисает над краем стола таким образом, что сила тяжести уравновешена силой трения (рисунок 3). В результате небольшого смещения ε цепочка начинает скользить. Определить время T, за которое цепочка полностью соскользнет со стола. Коэффициент трения между цепочкой и поверхностью стола равен μ
Решение.
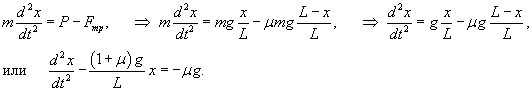 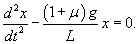 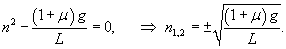 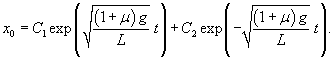 Построим теперь частное решение неоднородного уравнения. В правой части находится постоянное выражение, поэтому будем искать частное решение также в виде постоянного числа: 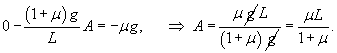 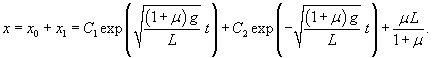 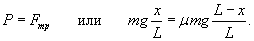 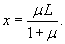 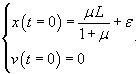 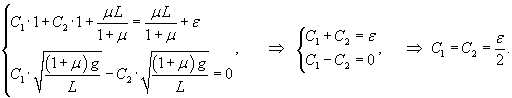 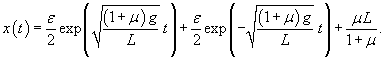 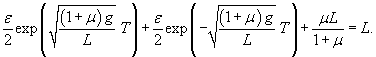 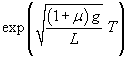 : :
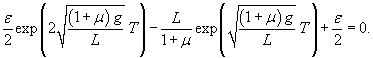 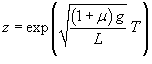 , приходим к квадратному уравнению: , приходим к квадратному уравнению:
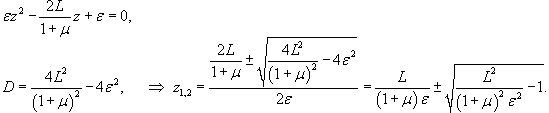 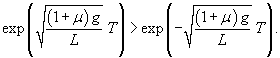 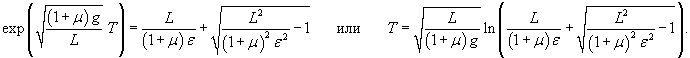 |
||||||
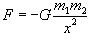 .
.
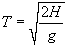 ;
;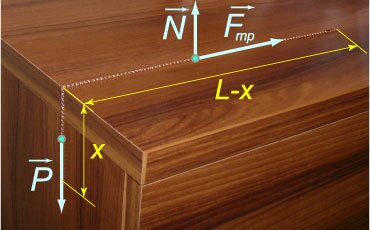
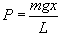 , где x − длина части цепочки, свисающей со стола, m − масса цепочки, L − ее длина, g − ускорение свободного падения;
, где x − длина части цепочки, свисающей со стола, m − масса цепочки, L − ее длина, g − ускорение свободного падения;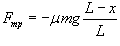 , где μ − коэффициент трения. Сила трения действует лишь на часть цепочки, лежащую на столе. Длина этой части равна
, где μ − коэффициент трения. Сила трения действует лишь на часть цепочки, лежащую на столе. Длина этой части равна