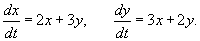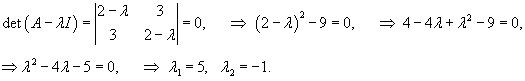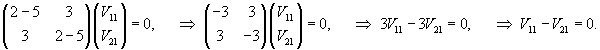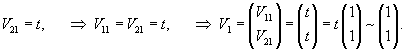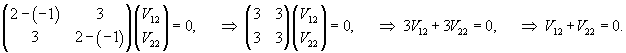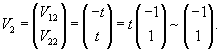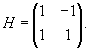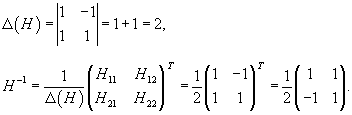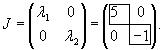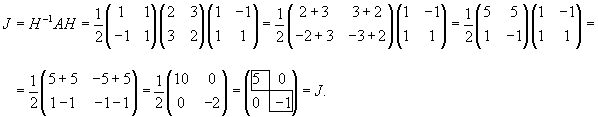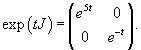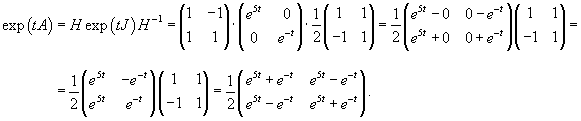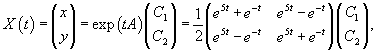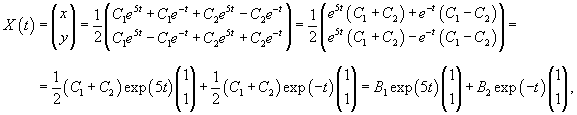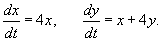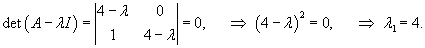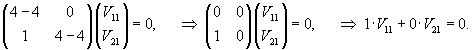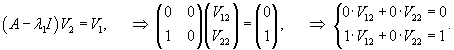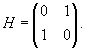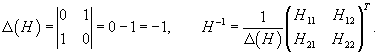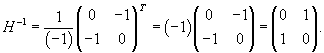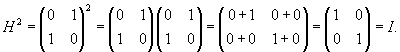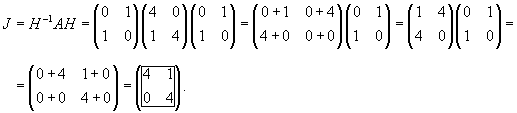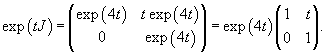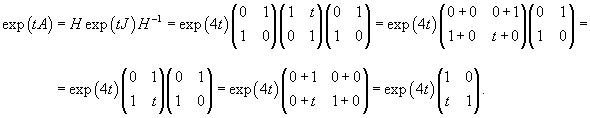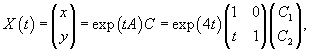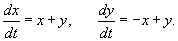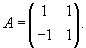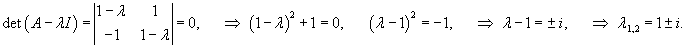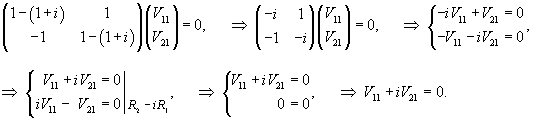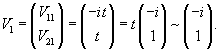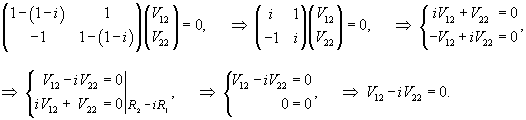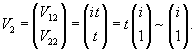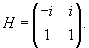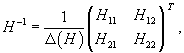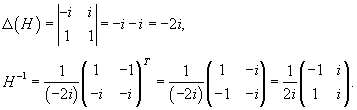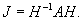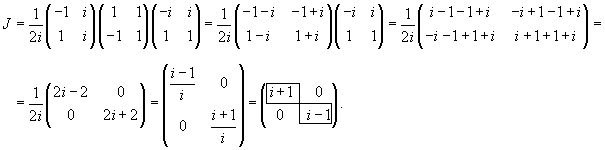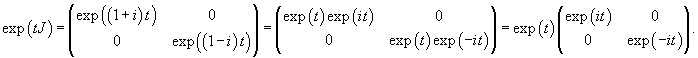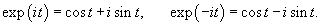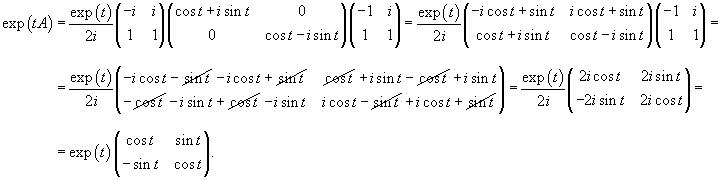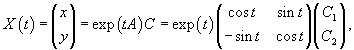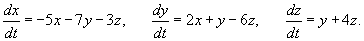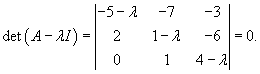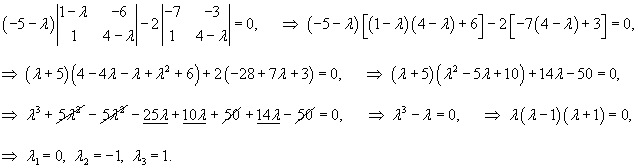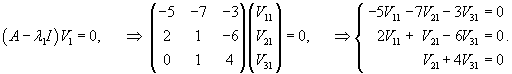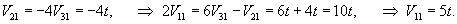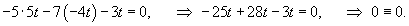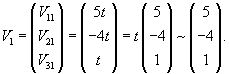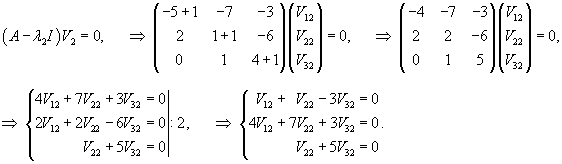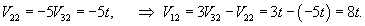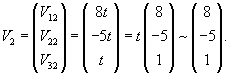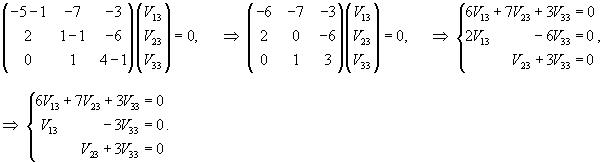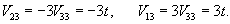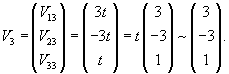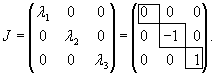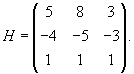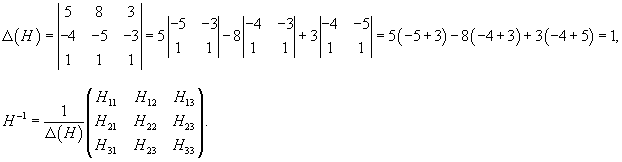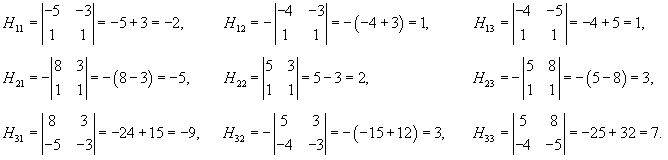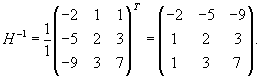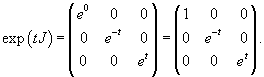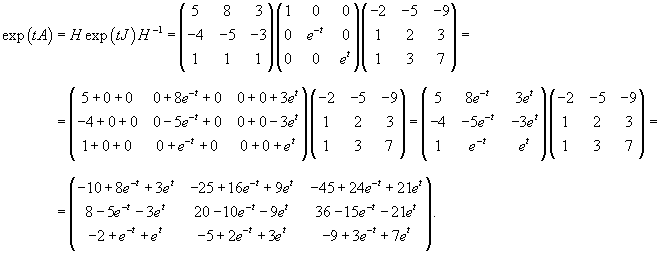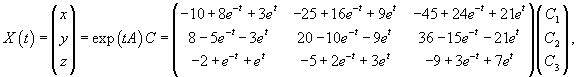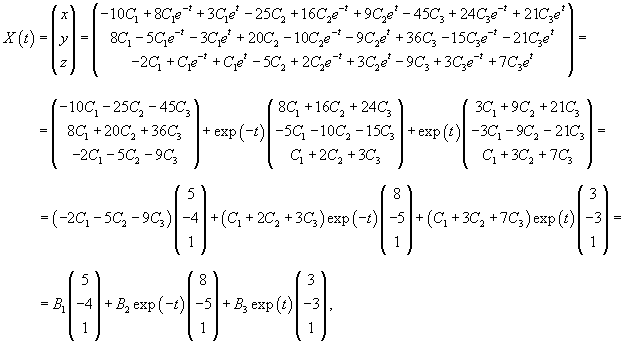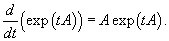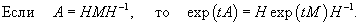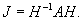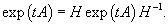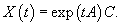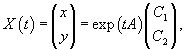|
|
|
|
Метод матричной экспоненты
|
|
Определение и свойства матричной экспоненты
Рассмотрим квадратную матрицу A размером n x n, элементы которой могут быть как действительными, так и комплексными числами. Поскольку матрица A квадратная, то для нее определена операция возведения в степень, т.е. мы можем вычислить матрицы
где через I обозначена единичная матрица порядка n.
Составим бесконечный матричный степенной ряд
Сумма данного бесконечного ряда называется матричной экспонентой и обозначается как exp (tA):
Этот ряд является абсолютно сходящимся.
В предельном случае, когда матрица состоит из одного числа a, т.е. имеет размер 1 x 1, приведенная формула превращается в известную формулу разложения экспоненциальной функции exp (at) в ряд Маклорена:
Матричная экспонента обладает следующими основными свойствами:
- Если A − нулевая матрица, то exp (tA) = exp (0) = I;
- Если A = I (I − единичная матрица), то exp (tI) = exp (t)I;
- Если для A существует обратная матрица A−1, то exp (A)exp (−A) = I;
- exp (mA)exp (nA) = exp ((m+n)A), где m, n − произвольные действительные или комплексные числа;
- Производная матричной экспоненты выражается формулой
- Пусть H − невырожденное линейное преобразование.
Применение матричной экспоненты для решения однородных линейных систем с постоянными коэффициентами
Матричная экспонента может успешно использоваться для решения систем дифференциальных уравнений. Рассмотрим систему линейных однородных уравнений, которая в матричной форме записывается в виде
Общее решение такой системы представляется через матричную экспоненту в виде
где C = (C1, C2, ..., Cn) T − произвольный n-мерный вектор. Символ T обозначает операцию транспонирования. В этой формуле мы не можем записать вектор C перед матричной экспонентой, поскольку произведение матриц 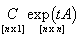 не определено.
Для задачи с начальными условиями (задачи Коши) компоненты вектора C выражаются через начальные условия. В этом случае решение однородной системы записывается в виде
Таким образом, решение однородной системы уравнений становится известным, если вычислена соответствующая матричная экспонента. Для ее вычисления можно воспользоваться бесконечным рядом, который содержится в определении матричной экспоненты. Однако часто это позволяет найти матричную экспоненту лишь приближенно. Для решения задачи можно использовать также алгебраический способ, основанный на последнем свойстве из перечисленных выше. Рассмотрим этот способ и общий ход решения более подробно.
Алгоритм решения системы уравнений методом матричной экспоненты
- Сначала находим собственные значения λi матрицы (линейного оператора) A;
- Вычисляем собственные и (в случае кратных собственных значений) присоединенные векторы;
- Из полученных собственных и присоединенных векторов составляем невырожденную матрицу линейного преобразования H. Вычисляем соответствующую обратную матрицу H −1;
- Находим нормальную жорданову форму J для заданной матрицы A, используя формулу
Примечание: В процессе нахождения собственных и присоединенных векторов часто становится ясной структура каждой жордановой клетки. Это позволяет сразу записать жорданову форму без вычисления по указанной формуле.
- Зная жорданову форму J, cоставляем матрицу exp (tJ). Соответствующие формулы для такого преобразования выводятся из определения матричной экспоненты. Для некоторых простых жордановых форм матрица exp (tJ) имеет вид, приведенный в таблице:
- Вычисляем матричную экспоненту exp (tA) по формуле
- Записываем общее решение системы, которое имеет следующий вид:
В случае систем дифференциальных уравнений 2-го порядка общее решение выражается формулой
где C1, C2 − произвольные постоянные.
|
|
Пример 1
|
|
Найти общее решение системы уравнений, используя матричную экспоненту:
Решение.
Решим данную систему, следуя описанному выше алгоритму. Вычислим собственные значения матрицы A:
Для каждого из собственных значений найдем собственные векторы. Для числа λ1 = 5 получаем:
Полагая V21 = t, находим собственный вектор V1 = (V11, V21) T:
Аналогично находим собственный вектор V2 = (V12, V22) T, ассоциированный с собственным значением λ2 = −1:
Пусть V22 = t. Тогда V12 = −V22 = −t. Следовательно,
Составим матрицу H из найденных собственных векторов V1 и V2:
Вычислим обратную матрицу H −1:
Поскольку в данном примере собственные числа являются простыми корнями характеристического уравнения, то можно сразу записать жорданову форму, которая будет иметь простой диагональный вид:
Проверим это, используя формулу перехода от исходной матрицы A к нормальной жордановой форме J:
Составим теперь матрицу (ее тоже можно назвать матричной экспонентой) exp (tJ):
Вычислим матричную экспоненту exp (tA):
Общее решение системы записывается в виде
где C1, C2 − произвольные числа.
Данный ответ можно выразить также и в другой форме:
где через B1 и B2 обозначены произвольные постоянные, связанные с C1, C2.
|
|
Пример 2
|
|
Решить систему уравнений методом матричной экспоненты:
Решение.
Решим характеристическое уравнение и найдем собственные значения:
Итак, мы имеем одно собственное значение λ1 = 4 кратностью 2. Определим собственный вектор V1 = (V11, V21) T:
Отсюда следует, что координата V11 = 0, а координата V21 может быть произвольной. Выберем для простоты V21 = 1. Следовательно, собственный вектор V1 равен: V1 = (0, 1) T.
Второй линейно независимый вектор определим как вектор V2 = (V12, V22) T, присоединенный к V1. Он находится из уравнения
Здесь координата V22 может быть любым числом. Выберем V22 = 0. Тогда получаем V11 = 1. Таким образом присоединенный вектор равен: V2 = (1, 0) T.
Теперь из найденных базисных векторов составим матрицу H − матрицу перехода от A к нормальной жордановой форме J:
Вычислим обратную матрицу H −1:
Здесь Hij обозначают алгебраические дополнения к элементам матрицы H. В результате вычислений находим:
Интересно, что в данном примере обратная матрица H −1 совпадает с исходной матрицей H. Такой эффект возможен, если квадрат исходной матрицы равен единичной матрице:
Жорданова форма J для матрицы A имеет вид:
Как видно, жорданова форма J состоит из одной клетки размером 2.
Составляем матрицу exp (tJ):
Вычисляем матричную экспоненту exp (tA):
Общее решение системы записывается как
где C1, C2 − произвольные константы.
|
|
Пример 3
|
|
Решить систему уравнений с помощью матричной экспоненты:
Решение.
В данном случае матрица коэффициентов A имеет вид:
Вычислим ее собственные значения:
Итак, матрица A имеет пару комплексно-сопряженных собственных значений. Для каждого собственного числа определим собственный вектор (он может иметь комплексные координаты).
Пусть числу λ1 = 1 + i соответствует собственный вектор V1 = (V11, V21) T. Координаты этого вектора удовлетворяют следующему матрично-векторному уравнению:
Полагаем V21 = t. Тогда V11 = −it. Следовательно, собственный вектор V1 равен:
Аналогично найдем собственный вектор V2 = (V12, V22) T, ассоциированный с числом λ2 = 1 − i :
Здесь полагаем V22 = t. Следовательно, V12 = it. Тогда вектор V2 будет равен:
Составляем матрицу H из найденных собственных векторов V1 и V2:
Вычисляем обратную матрицу H −1 по формуле
где Δ(H) − определитель матрицы H, Hij − алгебраические дополнения к элементам матрицы H. В результате получаем:
Теперь найдем нормальную жорданову форму J по формуле
Выполняя вычисления, находим:
Вообще говоря, мы могли бы сразу записать жорданову форму J, которая в данном случае имеет диагональный вид (поскольку собственные числа λ1, λ2 имеют кратность 1). Будем считать, что вычисление J сделано для проверки, а матрицы H и H −1 нам необходимы далее для определения матричной экспоненты.
Составим теперь матрицу exp (tJ):
Рассчитаем матричную экспоненту exp (tA):
Экспоненциальные функции exp (it), exp (−it) разложим по формуле Эйлера:
Получаем следующий результат:
Общее решение заданной системы уравнений выражается формулой
где C = (C1, C2) T − произвольный вектор.
|
|
Пример 4
|
|
Решить систему уравнений с помощью матричной экспоненты:
Решение.
Начнем решение с вычисления собственных значений:
Раскладываем определитель по первому столбцу:
Мы получили три собственных значения кратностью 1. Найдем для них соответствующие собственные векторы.
Пусть числу λ1 = 0 соответствует собственный вектор V1 = (V11, V21, V31) T. Определим его из следующего соотношения
Полагаем V31 = t. Выразим через t остальные координаты:
Можно проверить, что первое уравнение также соблюдается (поскольку оно является зависимым от других):
Итак, координаты собственного вектора V1 равны:
Аналогично найдем координаты второго вектора V2 = (V12, V22, V32) T, ассоциированного с числом λ2 = −1:
Здесь можно положить V32 = t. Тогда
Следовательно, собственный вектор V2 имеет такие координаты:
Наконец, найдем третий собственный вектор V3 = (V13, V23, V33) T, соответствующий собственному значению λ3 = 1:
Пусть V33 = t. Тогда
Следовательно, собственный вектор V3 равен
Зная собственные значения λ1, λ2, λ3, каждое из которых имеет кратность 1, можно записать жорданову форму J для матрицы A:
Составим матрицу H, столбцы которой образованы собственными векторами V1, V2, V3:
Вычислим обратную матрицу H −1. Обе матрицы H и H −1 понадобятся нам для нахождения матричной экспоненты. Получаем:
Алгебраические дополнения Hij имеют следующие значения:
Обратная матрица H −1 равна
Теперь мы имеем все необходимое, чтобы найти матричную экспоненту.
Зная жорданову матрицу J запишем матрицу exp (tJ):
Вычислим матричную экспоненту exp (tA):
Общее решение системы (в несколько громоздком виде) выражается формулой
где C = (C1, C2, C3) T − произвольный постоянный вектор.
Данный ответ можно представить в виде суммы, каждый член которой является произведением экспоненциальной функции с собственным значением λi и собственного вектора Vi :
где B = (B1, B2, B3) T − произвольный вектор.
|
|
|
|
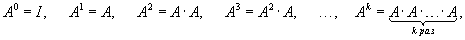
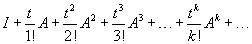
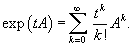
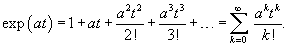
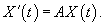
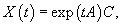
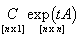 не определено.
не определено.