|
Линейные системы дифференциальных уравнений с переменными коэффициентами
|
|
Нормальная линейная система дифференциальных уравнений с переменными коэффициентами записывается в виде
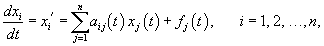 Используя векторно-матричные обозначения, данную систему уравнений можно записать как 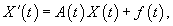 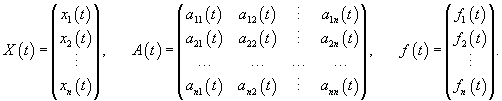 Соответствующая однородная система с переменными коэффициентами в векторной форме имеет вид 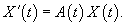
Фундаментальная система решений и фундаментальная матрица
Вектор-функции 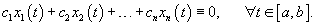 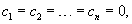 Любая система n линейно независимых решений Квадратная матрица Φ(t), столбцы которой образованы линейно независимыми решениями 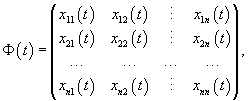 Заметим, что фундаментальная матрица Φ(t) является невырожденной, т.е. для нее всегда существует обратная матрица 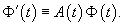 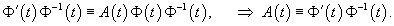 Общее решение однородной системы выражается через фундаментальную матрицу в виде 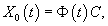 Упомянем один интересный частный случай однородных систем. Оказывается, если произведение матрицы A(t) и интеграла от этой матрицы коммутативно, т.е. 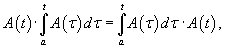 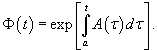
Определитель Вронского и формула Лиувилля-Остроградского
Определитель фундаментальной матрицы Φ(t) называется определителем Вронского или вронскианом системы решений 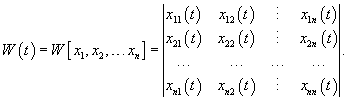
Для определителя Вронского системы решений 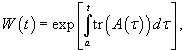 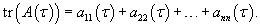
Метод вариации постоянных (метод Лагранжа)
Перейдем к рассмотрению неоднородных систем, которые в векторно-матричной форме записываются в виде
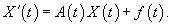 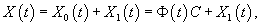 Наиболее общим методом решения неоднородных систем является метод вариации постоянных (метод Лагранжа). При использовании этого метода вместо постоянного вектора C мы рассматриваем вектор C(t), компоненты которого являются непрерывно дифференцируемыми функциями независимой переменной t, т.е. полагаем 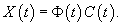 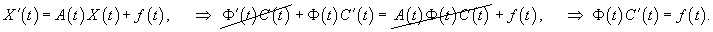 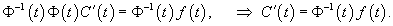 |
|
Пример 1
|
|
Составить линейную систему уравнений, имеющей решения
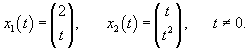
Решение.
В задаче задана фундаментальная матрица системы:
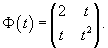 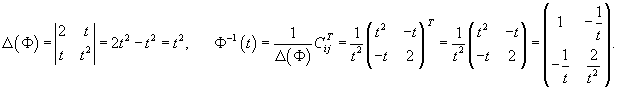 Матрица коэффициентов системы уравнений находится по формуле 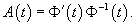 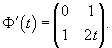 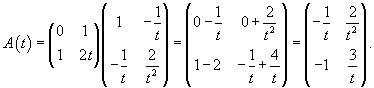 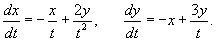 |
|
Пример 2
|
|
Найти фундаментальную матрицу системы дифференциальных уравнений
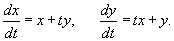
Решение.
Проверим сначала, что перемножение матрицы A(t) со своим интегралом коммутативно. Исходная матрица имеет вид:
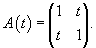 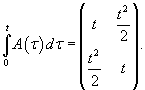 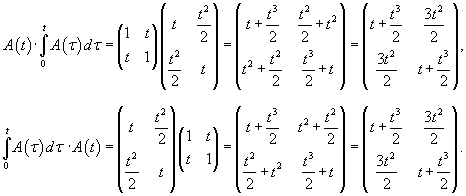 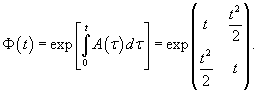 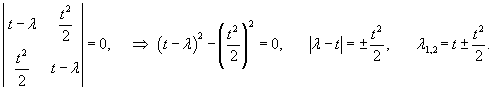 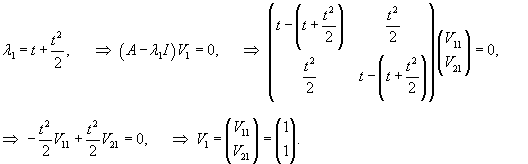 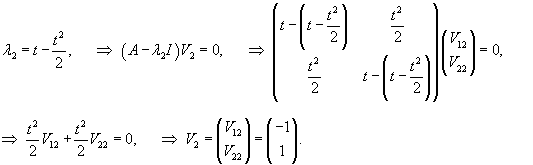 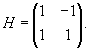 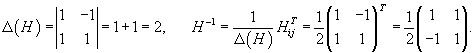 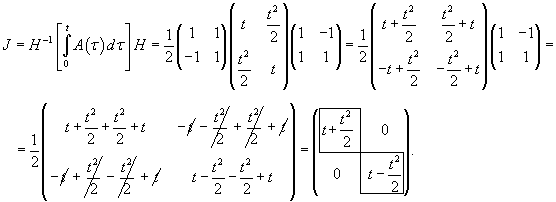 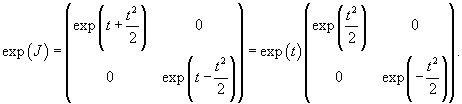 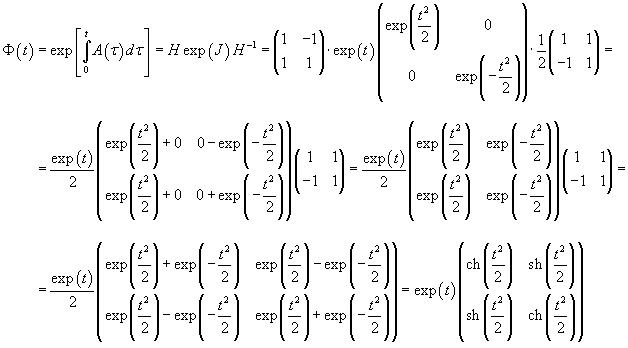 |
|
Пример 3
|
|
Найти общее решение системы
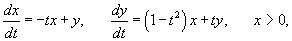 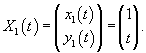
Решение.
Пусть второе линейно независимое решение выражается векторной функцией
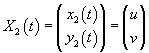 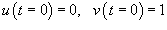 . .Воспользуемся формулой Лиувилля-Остроградского, которая записывается в виде: 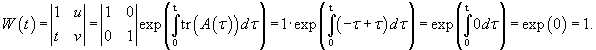 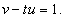 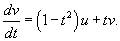 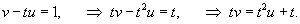 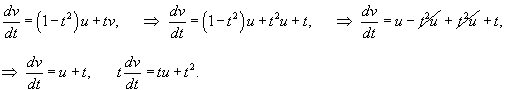 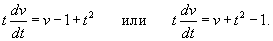  Теперь определим решение неоднородного уравнения, используя метод вариации постоянных: 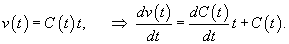 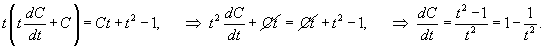 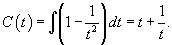 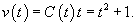 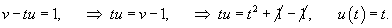 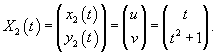 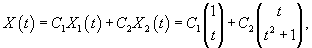 |
|
Пример 4
|
|
Найти общее решение линейной неоднородной системы уравнений
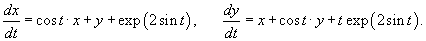
Решение.
Сначала построим общее решение однородной системы
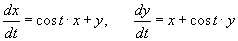 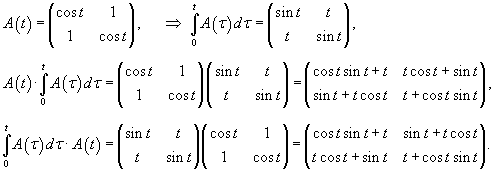 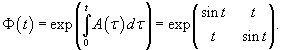 Определим собственные значения: 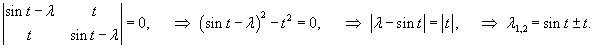  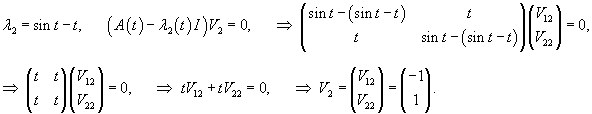 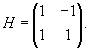 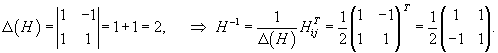 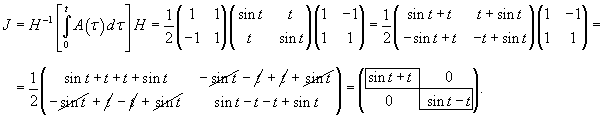 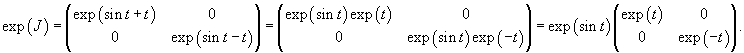 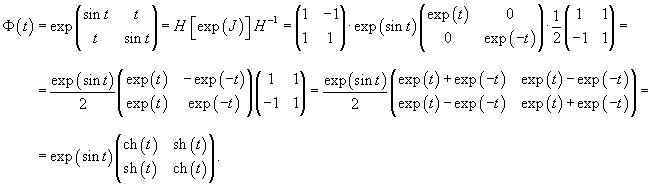 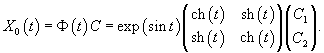 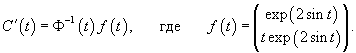 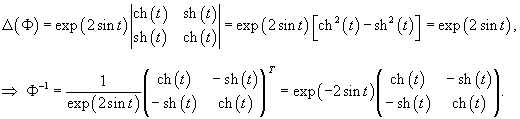 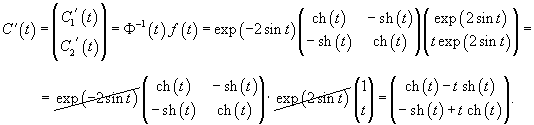 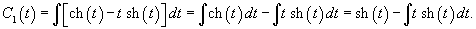 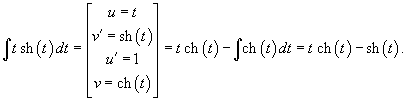  Аналогично находим функцию C2(t): 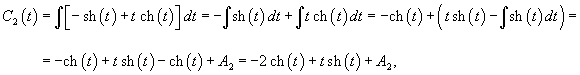 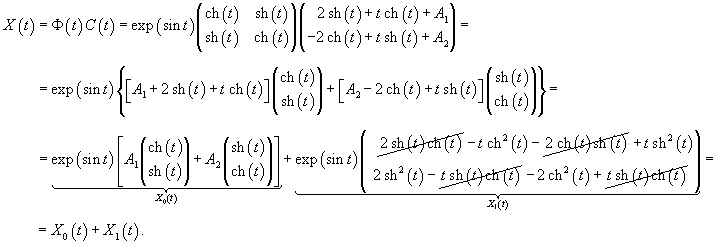 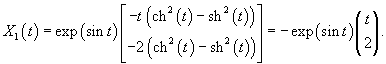 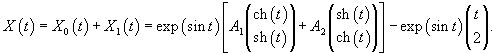 |