|
Интегрирование иррациональных функций
|
|
Для интегрирования иррациональной функции, содержащей
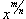 используется подстановка используется подстановка 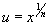 . .Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме 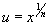 , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию. , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию.Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида 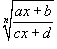 , интегрируется с помощью подстановки , интегрируется с помощью подстановки 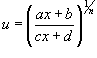 . .Интегрирование иррациональных функций, содержащих 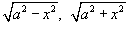 и и 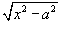 , рассматривается на странице Тригонометрические и гиперболические подстановки , рассматривается на странице Тригонометрические и гиперболические подстановки |
|
Пример 1
|
|
Найти интеграл
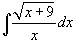 . .
Решение. 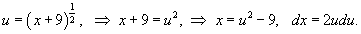 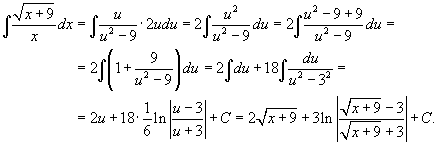 |
|
Пример 2
|
|
Вычислить интеграл
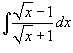 . .
Решение.  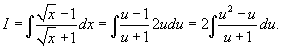 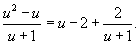  |
|
Пример 3
|
|
Вычислить интеграл
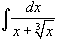 . .
Решение. 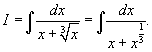 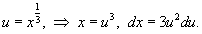 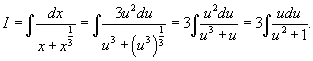 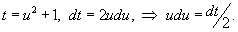 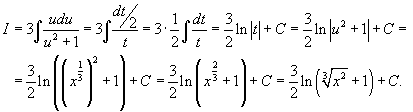 |
|
Пример 4
|
|
Вычислить интеграл
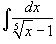 . .
Решение. 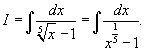 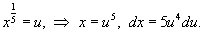 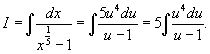 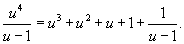 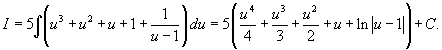 |
|
Пример 5
|
|
Вычислить интеграл
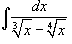 . .
Решение. 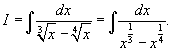 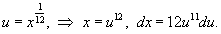 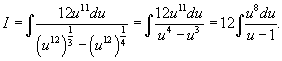 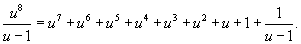 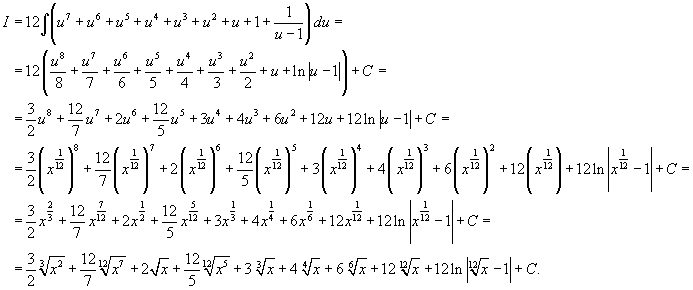 |
|
Пример 6
|
|
Вычислить интеграл
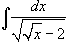 . .
Решение. 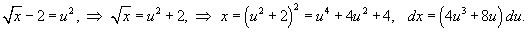 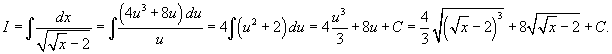 |
|
Пример 7
|
|
Вычислить интеграл
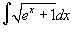 . .
Решение. 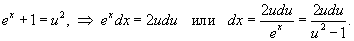  |