|
Раскрытие неопределенностей
|
|
Неопределенности типа Пусть заданы две функции 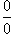 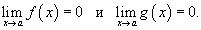 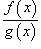 имеет неопределенность типа имеет неопределенность типа 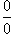 в точке в точке 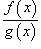 содержит неопределенность содержит неопределенность 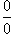 , нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю. , нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю.Примечание: В данном разделе при вычислении пределов не используется правило Лопиталя. Неопределенности типа Пусть две функции 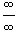 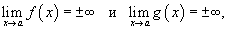 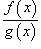 имеет в точке a неопределенность типа имеет в точке a неопределенность типа 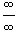 . Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени. . Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.Неопределенности типа Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа 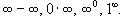 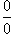 и и 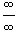 . . |
|
Пример 1
|
|
Вычислить предел
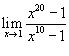 . .
Решение. 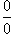 в точке в точке  |
|
Пример 2
|
|
Вычислить предел
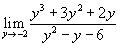 . .
Решение. 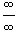 в точке в точке 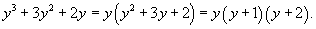 Аналогично, 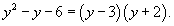 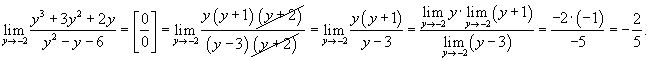 |
|
Пример 3
|
|
Вычислить предел
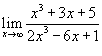 . .
Решение. 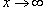 показывает, что функция имеет неопределенность типа показывает, что функция имеет неопределенность типа 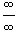 . Разделим числитель и знаменатель на x3 (x в наивысшей степени знаменателя). В результате получаем . Разделим числитель и знаменатель на x3 (x в наивысшей степени знаменателя). В результате получаем
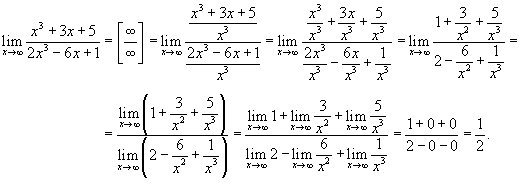 |
|
Пример 4
|
|
Вычислить предел
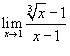 . .
Решение. 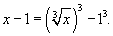 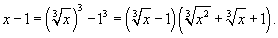 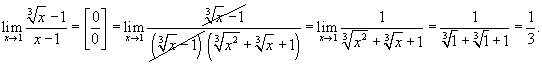 |
|
Пример 5
|
|
Вычислить предел
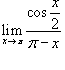 . .
Решение. 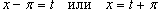 . Тогда . Тогда 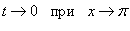 . Получаем . Получаем
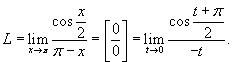 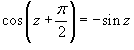 . В результате находим значение предела . В результате находим значение предела
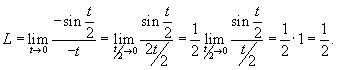 |
|
Пример 6
|
|
Вычислить предел
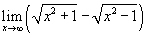 . .
Решение. 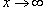 , то , то
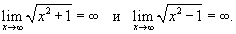  . Умножим и разделим данную иррациональную функцию на сопряженное выражение. . Умножим и разделим данную иррациональную функцию на сопряженное выражение.
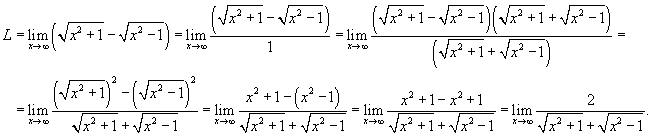 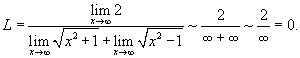 |
|
Пример 7
|
|
Найти предел
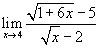 . .
Решение. 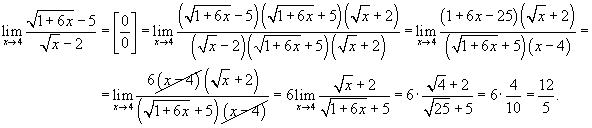 |
|
Пример 8
|
|
Найти предел
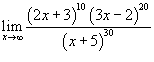 . .
Решение. 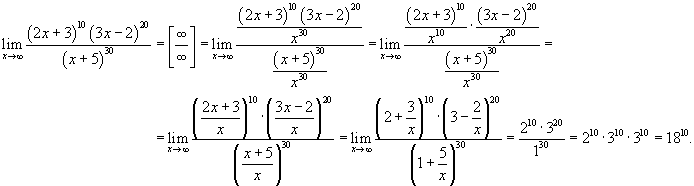 |
|
Пример 9
|
|
Найти предел
 . .
Решение.  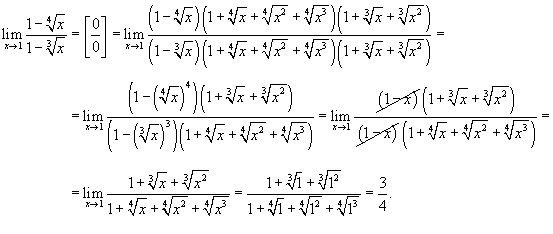 |
|
Пример 10
|
|
Найти предел
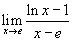 . .
Решение. 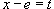 . Тогда . Тогда 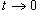 при при  . Следовательно, . Следовательно,
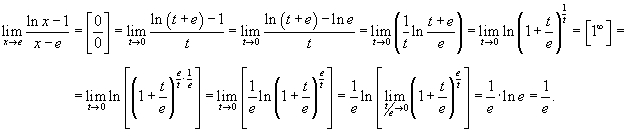 |
|
Пример 11
|
|
Найти предел
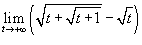 . .
Решение. 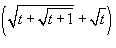 . Получаем . Получаем
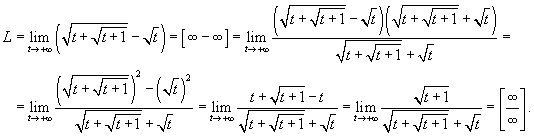 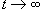 . Следовательно, разделим числитель и знаменатель на . Следовательно, разделим числитель и знаменатель на 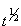 - то есть t в наивысшей степени знаменателя. Тогда - то есть t в наивысшей степени знаменателя. Тогда
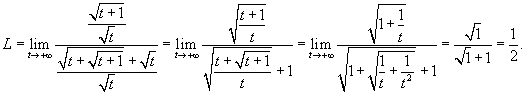 |
|
Пример 12
|
|
Найти предел
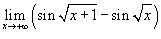 . .
Решение. 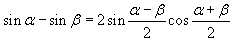 , перепишем предел в следующем виде , перепишем предел в следующем виде
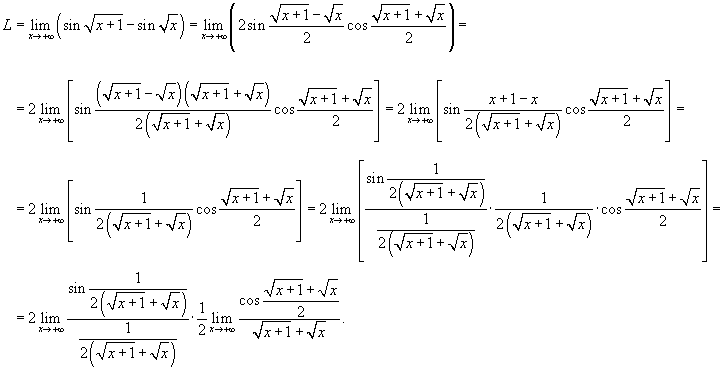 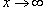 . Поэтому, окончательный ответ равен . Поэтому, окончательный ответ равен
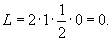 |