|
Правило Лопиталя
|
|||
|
Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность
типа  или или  . .Пусть a является некоторым конечным действительным числом или равно бесконечности.
 . Первые две неопределенности . Первые две неопределенности  можно свести к типу можно свести к типу  или или  с помощью алгебраических преобразований. А неопределенности с помощью алгебраических преобразований. А неопределенности  сводятся к типу сводятся к типу  с помощью соотношения с помощью соотношения
 |
|||
|
Пример 1
|
|||
|
Вычислить предел
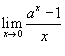 . .
Решение. 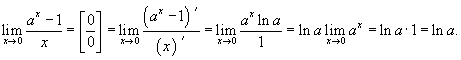 |
|||
|
Пример 2
|
|||
|
Вычислить предел
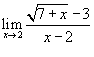 . .
Решение.  , применяем правило Лопиталя. , применяем правило Лопиталя.
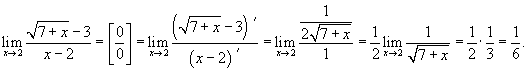 |
|||
|
Пример 3
|
|||
|
Вычислить предел
 . .
Решение.  . После простых преобразований, получаем . После простых преобразований, получаем
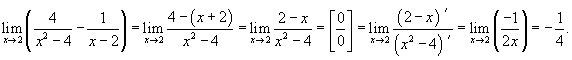 |
|||
|
Пример 4
|
|||
|
Найти предел
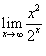 . .
Решение. 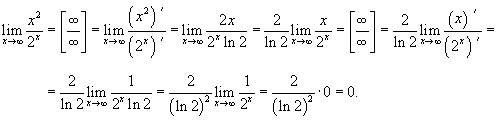 |
|||
|
Пример 5
|
|||
|
Найти предел
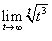 . .
Решение. 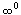 . Обозначим . Обозначим 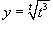 . После логарифмирования получаем . После логарифмирования получаем
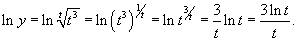 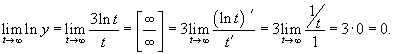 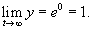 |
|||
|
Пример 6
|
|||
|
Найти предел
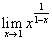 . .
Решение. 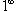 . Пусть . Пусть 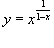 . Тогда . Тогда
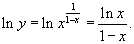 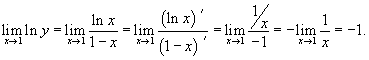 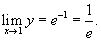 |
|||
|
Пример 7
|
|||
|
Вычислить предел
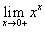 . .
Решение. 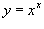 . Возьмем логарифм от обеих частей: . Возьмем логарифм от обеих частей:
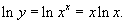 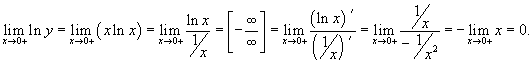 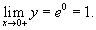 |
|||
|
Пример 8
|
|||
|
Вычислить предел
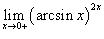 . .
Решение. 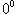 . Пусть . Пусть 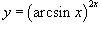 . Тогда после логарифмирования получаем . Тогда после логарифмирования получаем
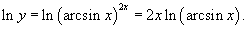 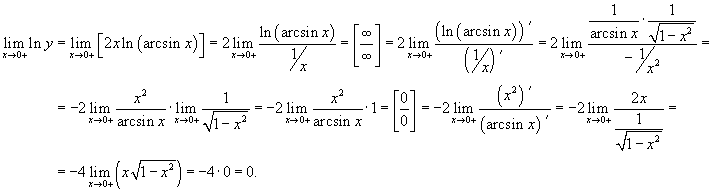 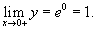 |
|||
|
Пример 9
|
|||
|
Найти предел
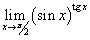 . .
Решение. 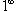 . Обозначим . Обозначим  . Прологарифмируем обе части этого равенства. . Прологарифмируем обе части этого равенства.
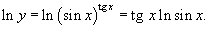 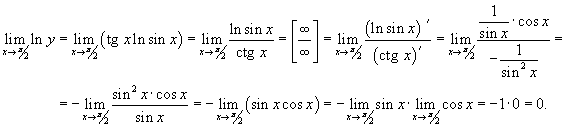 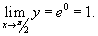 |
|||
|
Пример 10
|
|||
|
Найти предел
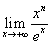 . .
Решение.  . Применяем правило Лопиталя n раз. . Применяем правило Лопиталя n раз.
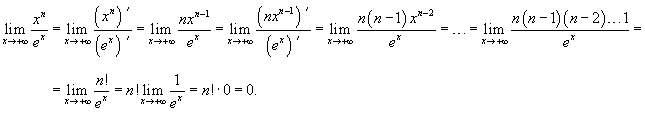 |
|||
|
Пример 11
|
|||
|
Вычислить предел
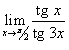 . .
Решение. 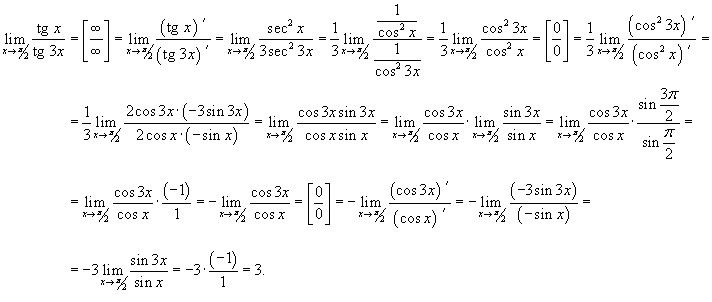 |
|||
|
Пример 12
|
|||
|
Вычислить предел
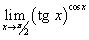 . .
Решение. 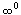 . Пусть . Пусть 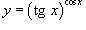 . Тогда . Тогда
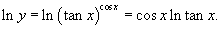 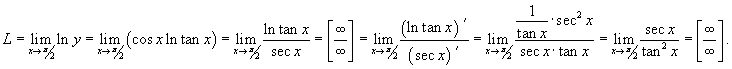 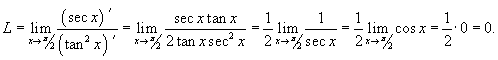 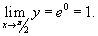 |
|||
 и
и  , то
, то  ;
; и
и  , то аналогично
, то аналогично  .
.