|
Уравнения, не разрешенные относительно производной
|
|
Определение и методы решения
Уравнение вида
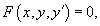 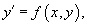 Далее мы предполагаем, что дифференциальное уравнение не приводится к явной форме. Основной метод решения таких неявных уравнений − это метод введения параметра. Ниже мы покажем, как этот метод используется для нахождения общего решения для некоторых важных частных случаев уравнений, не разрешенных относительно производной. Отметим, что общее решение может не покрывать все возможные решения дифференциального уравнения. Помимо общего решения, дифференциальное уравнение может также содержать так называемые особые решения. Более детально это рассматривается на странице Особые решения дифференциальных уравнений.
Случай 1. Уравнение вида x=f(y,y').
В этом случае переменная x выражается явно через переменную y и ее производную y'. Введем параметр 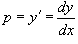 . Продифференцируем уравнение . Продифференцируем уравнение 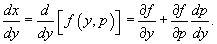  , то последнее выражение можно переписать в виде: , то последнее выражение можно переписать в виде:
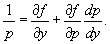 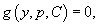 Таким образом, общее решение исходного дифференциального уравнения определяется в параметрической форме системой двух алгебраических уравнений: 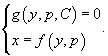
Случай 2. Уравнение вида y=f(x,y').
Здесь мы встречаемся с похожим случаем, но теперь переменная y явно зависит от x и y'. Введем параметр 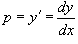 и продифференцируем уравнение и продифференцируем уравнение 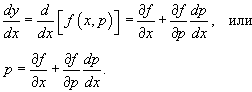 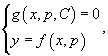
Case 3. Уравнение вида x=f(y').
В данном случае дифференциальное уравнение не содержит переменную y. Используя параметр 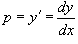 , легко построить общее решение уравнения. Так как , легко построить общее решение уравнения. Так как 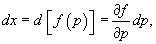 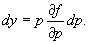 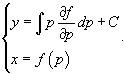
Случай 4. Уравнение вида y=f(y').
Уравнение такого типа не содержит переменную x и решается аналогичным образом. Используя параметр 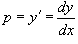 , можно записать: , можно записать: 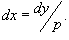 Отсюда следует, что Отсюда следует, что
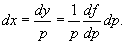 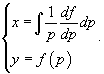 |
|
Пример 1
|
|
Найти общее решение уравнения
Решение. 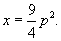 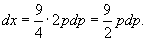  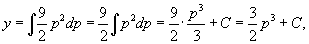 Таким образом, мы получили общее решение уравнения в параметрической форме: 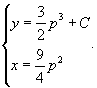 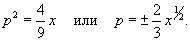 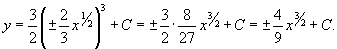 |
|
Пример 2
|
|
Найти общее решение дифференциального уравнения
Решение. 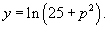 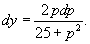 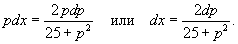 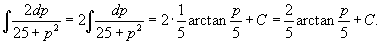 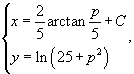 |
|
Пример 3
|
|
Решить дифференциальное уравнение
Решение. 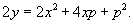 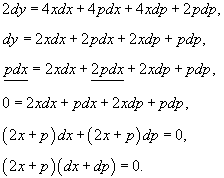 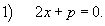 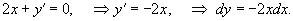 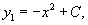 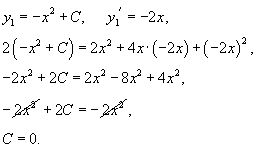 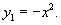 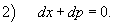 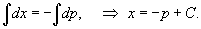 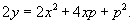 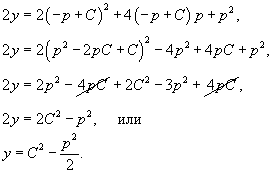 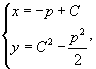 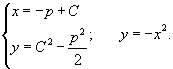 |