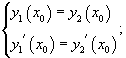|
Особые решения дифференциальных уравнений
|
||||||||||||||||||
|
Определение особого решения
Функция Примечание: Иногда используется более слабое определение особого решения, когда единственность решения нарушается лишь в некоторых точках. Особое решение дифференциального уравнения не описывается общим интегралом. Поэтому, оно не выводится из общего решения ни при каком значении постоянной C. Это можно проиллюстрировать следующим примером: Пусть требуется решить уравнение
p-дискриминант
Одним из способов нахождения особого решения является исследование так называемого p-дискриминанта дифференциального уравнения. Если функция 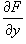 , , 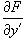 непрерывны в области определения дифференциального уравнения, то особое решение находится из системы уравнений: непрерывны в области определения дифференциального уравнения, то особое решение находится из системы уравнений:
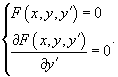 После нахождения p-дискриминантной кривой необходимо проверить следующее:
Огибающая семейства интегральных кривых и C-дискриминант
Другой способ нахождения особого решения в виде огибающей семейства интегральных кривых основан на использовании C-дискриминанта.Пусть 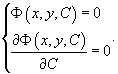
Общий алгоритм нахождения особых точек
Более общий способ нахождения особых точек дифференциального уравнения основан на одновременном использовании p-дискриминанта и C-дискриминанта.Сначала мы определяем уравнения p-дискриминанта и C-дискриминанта:
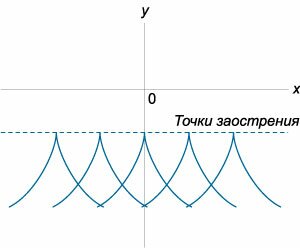
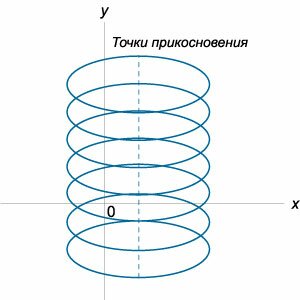
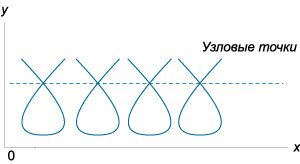
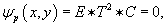 Аналогично, уравнение C-дискриминанта также раскладывается на произведение трех функций: 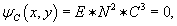 Здесь мы имеем дело с новыми типами особых точек: C - точки заострения, T - точки прикосновения и N - узловые точки. Их вид в плоскости xy схематически представлен на рисунках 2-4.
|
||||||||||||||||||
|
Пример 1
|
||||||||||||||||||
|
Найти особые решения уравнения
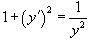 . .
Решение. 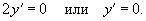  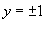 . Легко проверить, что это решение удовлетворяет дифференциальному уравнению: . Легко проверить, что это решение удовлетворяет дифференциальному уравнению:
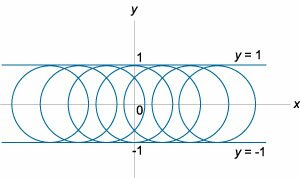
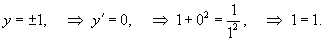 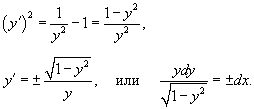 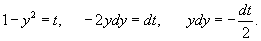 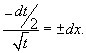 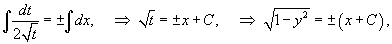 Последнее выражение можно записать в следующем виде: 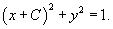 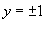 являются огибающими для данного семейства окружностей. Однако необходимо формально проверить, что на этих прямых нарушается единственность решения. являются огибающими для данного семейства окружностей. Однако необходимо формально проверить, что на этих прямых нарушается единственность решения.Возьмем произвольную точку x0. Запишем условие касания двух интегральных кривых в этой точке: 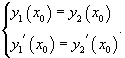 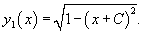 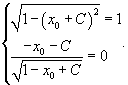 Таким образом, мы доказали, что в каждой точке x0 прямой линии |
||||||||||||||||||
|
Пример 2
|
||||||||||||||||||
|
Найти особое решение дифференциального уравнения
Решение. 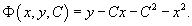 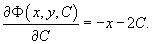 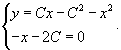 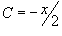 . Подставляя это в первое уравнение, находим C-дискриминантную кривую, которая является параболой: . Подставляя это в первое уравнение, находим C-дискриминантную кривую, которая является параболой:
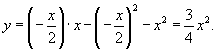 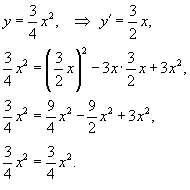 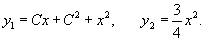 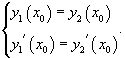 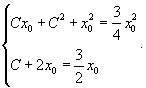 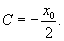 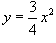 является огибающей (т.е. особым решением) для семейства парабол является огибающей (т.е. особым решением) для семейства парабол |
||||||||||||||||||
|
Пример 3
|
||||||||||||||||||
|
Исследовать особые решения дифференциального уравнения
Решение. 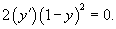 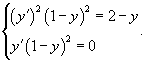 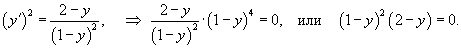 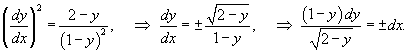 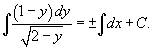 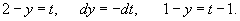 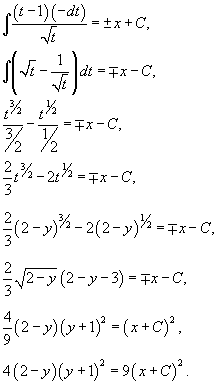 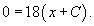 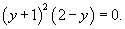 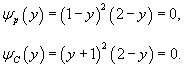 Из выражения для p-дискриминанта можно также определить уравнение точек прикосновения: 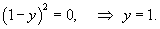 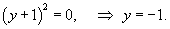 |
||||||||||||||||||