|
Формула Грина
|
||||||
|
Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция
  . Тогда справедлива формула Грина . Тогда справедлива формула Грина
  указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки.Если  , то формула Грина принимает вид , то формула Грина принимает вид
 Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией   называется вектор, обозначаемый называется вектор, обозначаемый  или или  и равный и равный
  |
||||||
|
Пример 1
|
||||||
|
Используя формулу Грина, вычислить интеграл
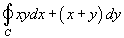 , где кривая C − окружность радиуса R. , где кривая C − окружность радиуса R.
Решение. 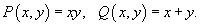 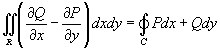 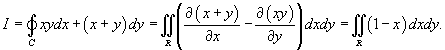 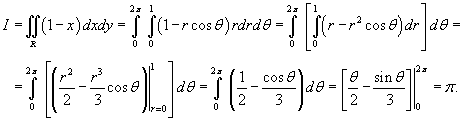 |
||||||
|
Пример 2
|
||||||
|
Используя формулу Грина, найти интеграл
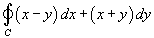 , где кривая C представляет собой окружность, заданную уравнением , где кривая C представляет собой окружность, заданную уравнением 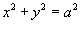 . .
Решение. 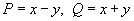 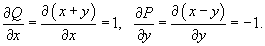 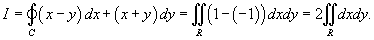 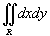 численно равен площади круга численно равен площади круга 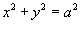 , то есть , то есть 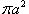 . Тогда интеграл равен . Тогда интеграл равен
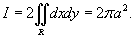 |
||||||
|
Пример 3
|
||||||
|
Используя формулу Грина, вычислить интеграл
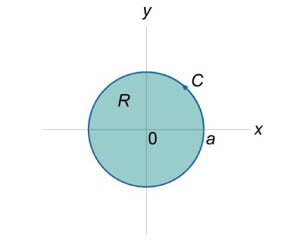
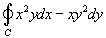 . Кривая C представляет собой окружность . Кривая C представляет собой окружность 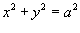 (рисунок 1), обход которой производится против часовой стрелки. (рисунок 1), обход которой производится против часовой стрелки.
Решение. 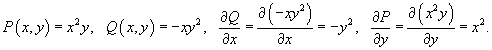 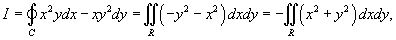 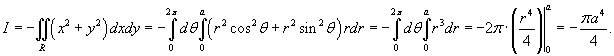
|
||||||
|
Пример 4
|
||||||
|
Используя формулу Грина, найти интеграл
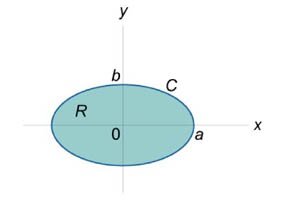
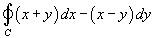 , где кривая C представляет собой эллипс , где кривая C представляет собой эллипс 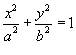 (рисунок 2). (рисунок 2).
Решение. 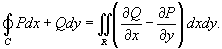 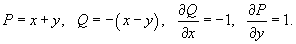 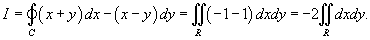 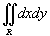 численно равен площади эллипса численно равен площади эллипса 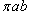 , то интеграл равен , то интеграл равен
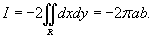 |
||||||
|
Пример 5
|
||||||
|
С помощью формулы Грина вычислить интеграл
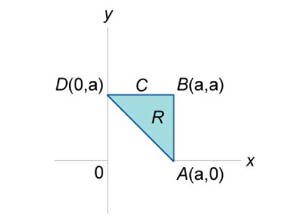
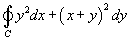 , где контур C представляет собой треугольник ABD с вершинами , где контур C представляет собой треугольник ABD с вершинами Решение. 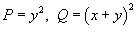 , так что , так что
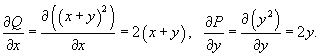 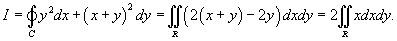 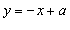 . Следовательно, полученный двойной интеграл вычисляется следующим образом . Следовательно, полученный двойной интеграл вычисляется следующим образом
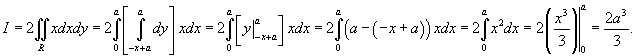
|
||||||
|
Пример 6
|
||||||
|
С помощью формулы Грина найти интеграл
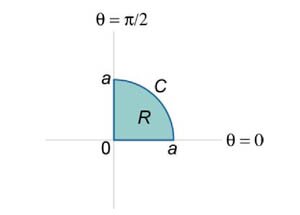
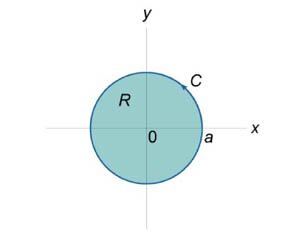
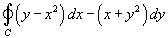 . Контур C ограничивает сектор круга радиусом a, лежащий в первом квадранте (рисунок 4). . Контур C ограничивает сектор круга радиусом a, лежащий в первом квадранте (рисунок 4).
Решение. 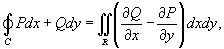 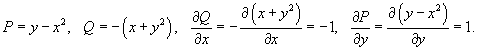 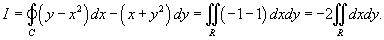 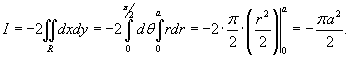 |
||||||
|
Пример 7
|
||||||
|
Вычислить интеграл
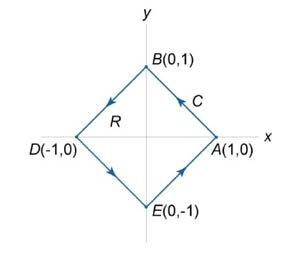
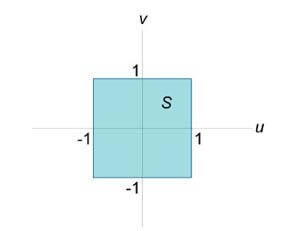
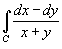 с использованием формулы Грина. Контур интегрирования C представляет собой квадрат с вершинами в точках с использованием формулы Грина. Контур интегрирования C представляет собой квадрат с вершинами в точках Решение. 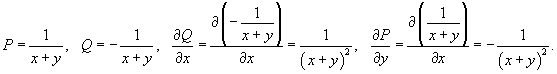 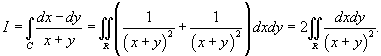 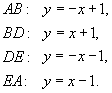 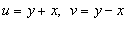 . Уравнения сторон квадрата записываются через новые переменные u и v в виде . Уравнения сторон квадрата записываются через новые переменные u и v в виде
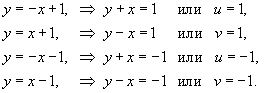 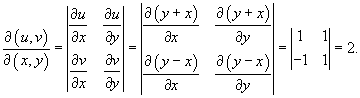 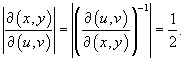 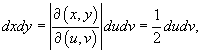 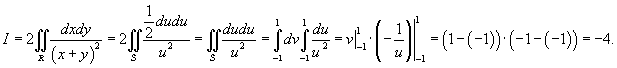
|
||||||
|
Пример 8
|
||||||
|
Вычислить интеграл
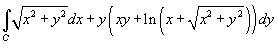 с помощью формулы Грина. Контур интегрирования C представляет собой окружность с помощью формулы Грина. Контур интегрирования C представляет собой окружность 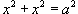 (рисунок 7). (рисунок 7).
Решение. 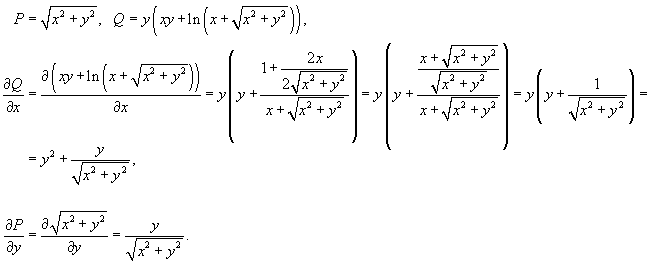 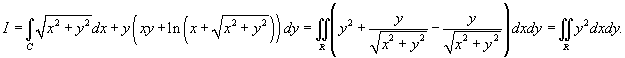 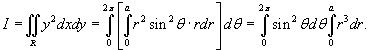 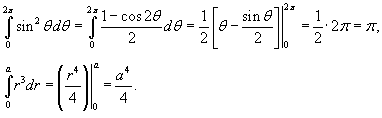 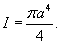
|
||||||
|
Пример 9
|
||||||
|
Найти площадь области R, ограниченной астроидой
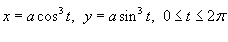 . .
Решение. 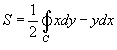 . Запишем данную формулу в параметрическом виде: . Запишем данную формулу в параметрическом виде:
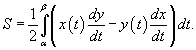 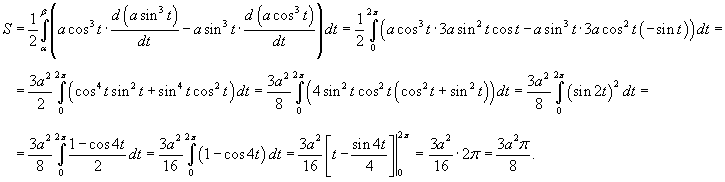 |
||||||
|
Пример 10
|
||||||
|
Проверить формулу Грина для векторного поля
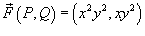 и области интегрирования R, имеющей форму круга радиусом 2 с центром в начале координат. и области интегрирования R, имеющей форму круга радиусом 2 с центром в начале координат.
Решение. 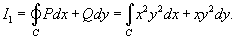 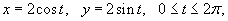 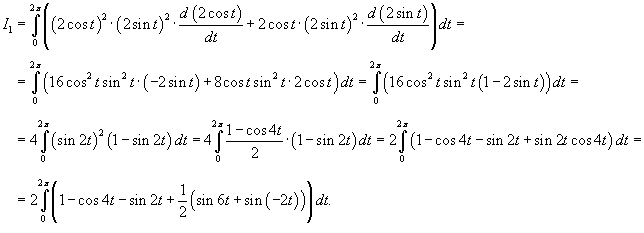 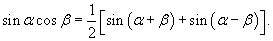 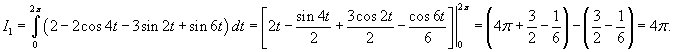 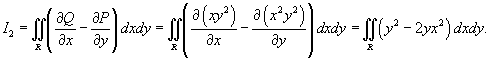 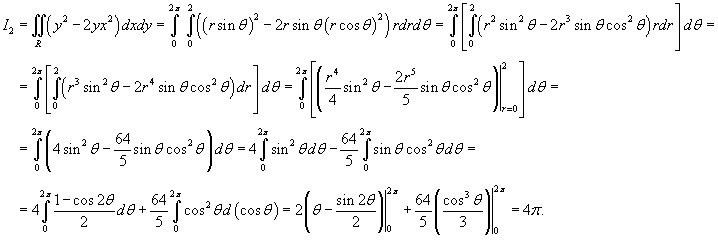 |
||||||