|
Теорема Стокса
|
||||||
|
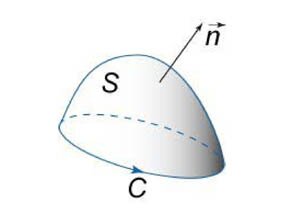
Пусть S является гладкой поверхностью, ограниченной гладкой кривой C. Тогда для любой непрерывно дифференцируемой векторной функции
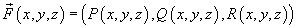 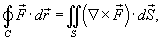 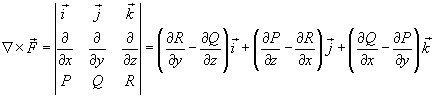 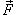 . .Символ 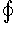 показывает, что криволинейный интеграл вычисляется по замкнутой кривой. показывает, что криволинейный интеграл вычисляется по замкнутой кривой.Будем предполагать, что ориентация поверхности и направление обхода кривой соответствуют правилу правой руки. В этом случае при обходе кривой поверхность всегда остается слева, если голова направлена в ту же сторону, что и вектор нормали 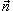 (рисунок 1). (рисунок 1).Теорема Стокса связывает между собой криволинейные интегралы второго рода и поверхностные интегралы второго рода. В координатной форме теорема Стокса может быть записана в следующем виде: 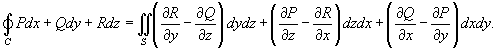
|
||||||
|
Пример 1
|
||||||
|
Показать, что криволинейный интеграл
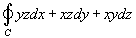 равен 0 вдоль любого замкнутого контура C. равен 0 вдоль любого замкнутого контура C.
Решение. 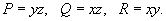 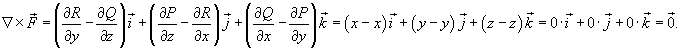 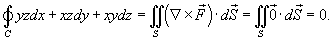 |
||||||
|
Пример 2
|
||||||
|
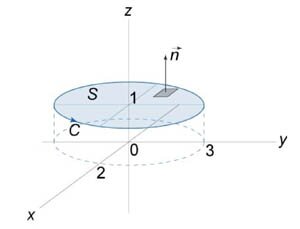
Используя формулу Стокса, вычислить криволинейный интеграл
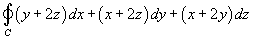 , где кривая C образована пересечением сферы , где кривая C образована пересечением сферы 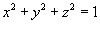 плоскостью плоскостью 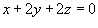 . .
Решение.  к поверхности S: к поверхности S:
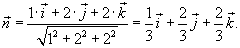 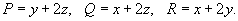 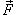 равен равен
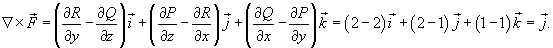 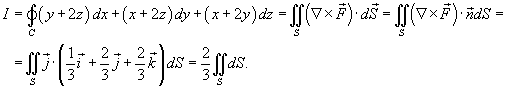 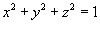 находится в начале координат, а плоскость находится в начале координат, а плоскость 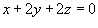 также проходит через начало координат, то сечением будет являться круг радиусом 1. Тогда интеграл имеет значение также проходит через начало координат, то сечением будет являться круг радиусом 1. Тогда интеграл имеет значение
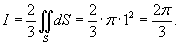 |
||||||
|
Пример 3
|
||||||
|
Используя теорему Стокса, найти криволинейный интеграл
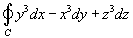 . Кривая C представляет собой пересечение цилиндра . Кривая C представляет собой пересечение цилиндра 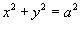 и плоскости и плоскости 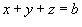 . .
Решение. 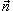 , координаты которого равны , координаты которого равны
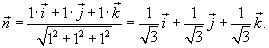 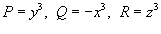 , то можно записать , то можно записать
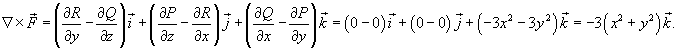 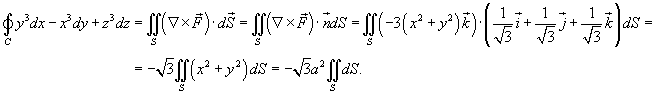 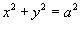 радиуса a. Поэтому, записывая уравнение плоскости в виде радиуса a. Поэтому, записывая уравнение плоскости в виде 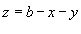 и используя формулу и используя формулу
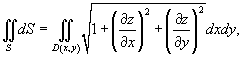 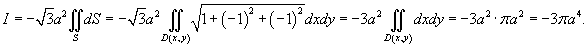 |
||||||
|
Пример 4
|
||||||
|
Вычислить криволинейный интеграл
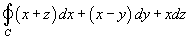 , используя теорему Стокса. Кривая C имеет форму эллипса и определяется уравнениями , используя теорему Стокса. Кривая C имеет форму эллипса и определяется уравнениями 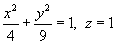 (рисунок 2 выше). (рисунок 2 выше).
Решение. 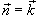 . Поскольку . Поскольку
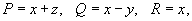 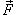 равен равен
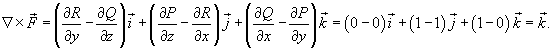  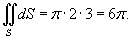 |
||||||
|
Пример 5
|
||||||
|
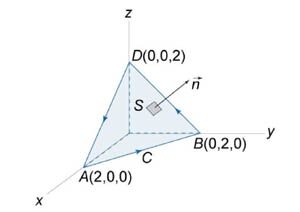
Используя теорему Стокса, вычислить криволинейный интеграл
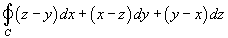 . Кривая C представляет собой треугольник с вершинами . Кривая C представляет собой треугольник с вершинами Решение. Определим сначала нормальный вектор 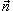 : :
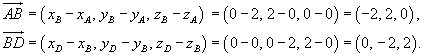 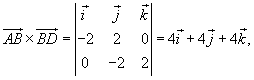 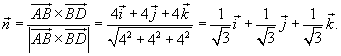 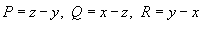 , и ротор , и ротор 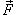 равен равен
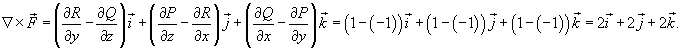 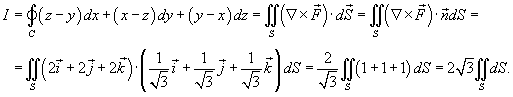  равен площади треугольника ABD, которая составляет равен площади треугольника ABD, которая составляет
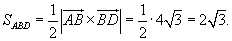 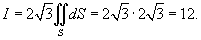
|
||||||
|
Пример 6
|
||||||
|
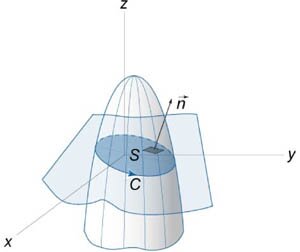
Найти интеграл
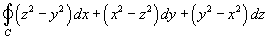 с использованием теоремы Стокса. Кривая C образована пересечением параболоида с использованием теоремы Стокса. Кривая C образована пересечением параболоида 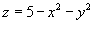 с плоскостью с плоскостью 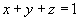 . (рисунок 4). . (рисунок 4).
Решение. 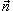 : :
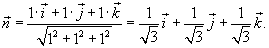 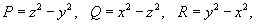 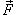 равен равен
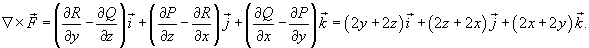 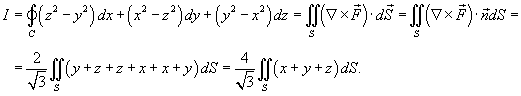 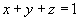 , то интеграл становится равным , то интеграл становится равным
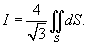  , то есть найти площадь поверхности S. , то есть найти площадь поверхности S.Явное уравнение плоскости имеет вид 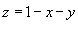 . Поэтому, по формуле . Поэтому, по формуле
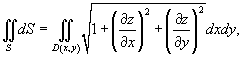 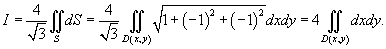 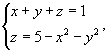 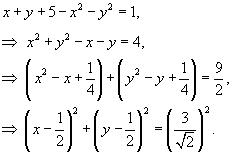 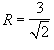 с центром в точке с центром в точке 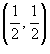 . Тогда площадь области . Тогда площадь области 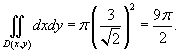 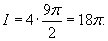 |
||||||