|
Сходимость рядов Фурье
|
|||||||||||||||
|
Некоторые определения
Говорят, что функция
Частичные суммы ряда Фурье
Введем понятие частичной суммы ряда Фурье 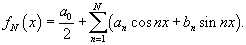 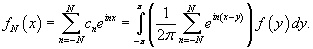
Ядро Дирихле
Функция
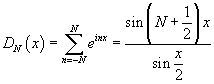 Частичная сумма ряда Фурье выражается через ядро Дирихле следующим образом: 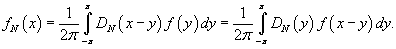
Сходимость ряда Фурье в точке
Пусть 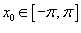
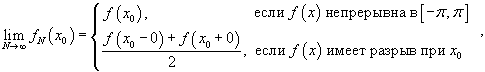
Равномерная сходимость ряда Фурье
Говорят, что последовательность частичных сумм ряда Фурье 
Сходимость ряда Фурье в пространстве L2
Пространство 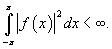 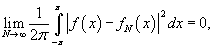 Из равномерной сходимости ряда Фурье следует как сходимость в точке, так и сходимость в пространстве L2. Обратное утверждение неверно: сходимость в пространстве L2 не означает, что ряд Фурье сходится в точке или равномерно, и, аналогично, из сходимости в точке не вытекает равномерная сходимость или сходимость в пространстве L2.
Явление Гиббса
Если функция имеет разрыв второго рода в некоторой точке, то частичные суммы ряда Фурье будут осциллировать вблизи этой точки (смотрите рисунок 4 выше). Этот эффект называется феноменом или явлением Гиббса. В любой точке разрыва второго рода амплитуда выбросов примерно на 18% (при 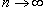 ) превышает амплитуду скачка функции в точке разрыва. ) превышает амплитуду скачка функции в точке разрыва. |
|||||||||||||||
|
Пример 1
|
|||||||||||||||
|
Вычислить интеграл
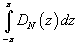 . .
Решение. 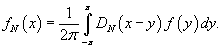 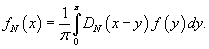 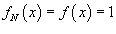 , подставим данную функцию в последнюю формулу. Получим , подставим данную функцию в последнюю формулу. Получим
 Найдем новые пределы интегрирования: если В результате получаем 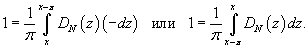 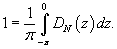 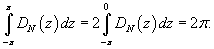 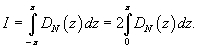 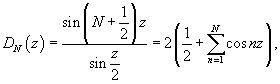 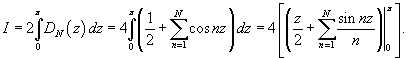 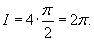 |
|||||||||||||||
|
Пример 2
|
|||||||||||||||
|
Пусть функция
 определена в интервале определена в интервале Решение.     , получим знакопеременный ряд для , получим знакопеременный ряд для  : :
  |
|||||||||||||||
|
Пример 3
|
|||||||||||||||
|
Доказать, что ряд Фурье функции
 сходится равномерно к сходится равномерно к Решение.  в ряд Фурье в заданном интервале имеет вид: в ряд Фурье в заданном интервале имеет вид:
 Соответственно, частичные суммы определяются соотношением      . . |
|||||||||||||||
|
Пример 4
|
|||||||||||||||
|
Доказать, что ряд Фурье функции
Решение. 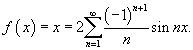 Тогда частичные суммы определяются выражением 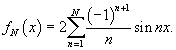 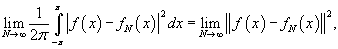 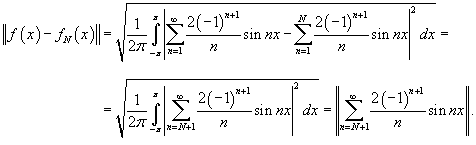 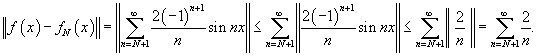 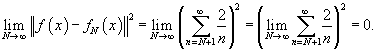 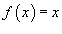 сходится в смысле среднеквадратичного к самой функции. сходится в смысле среднеквадратичного к самой функции. |
|||||||||||||||
|
Пример 5
|
|||||||||||||||
|
Известно, что ряд Фурье функции
 , заданной в интервале , заданной в интервале  (смотрите пример 2 выше). Исследовать поведение частичных сумм (смотрите пример 2 выше). Исследовать поведение частичных сумм Решение. 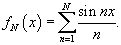
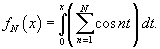 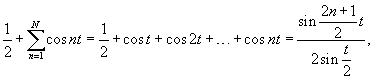 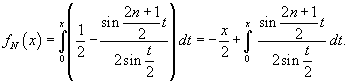 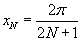 . Тогда . Тогда
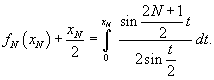 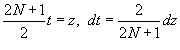 . Здесь . Здесь 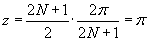 при при 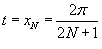 . Следовательно, получаем . Следовательно, получаем
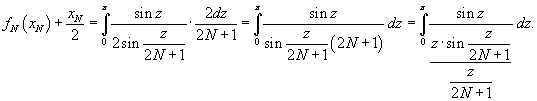 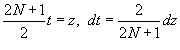 при при 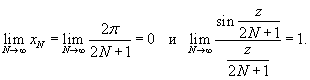 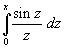 называется интегральным синусом и обозначается как называется интегральным синусом и обозначается как
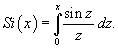 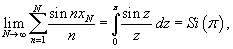 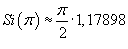 . .Как видно, амплитуда выброса вследствие эффекта Гиббса составляет примерно 18%. |
|||||||||||||||







