|
Сходимость рядов. Признаки сравнения
|
|
Необходимый признак сходимости, вообще говоря, не гарантирует сходимости ряда. Сходимость или расходимость ряда устанавливается с помощью достаточных признаков. Признаки сравнения, которые мы рассмотрим ниже, как раз и представляют собой достаточные признаки сходимости или расходимости рядов.
Признаки сравнения рядов
Даны два ряда  и и  − такие, что − такие, что  для всех n. Тогда справедливы следующие признаки: для всех n. Тогда справедливы следующие признаки:
Предельные признаки сравнения рядов
Пусть даны два ряда  и и  , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки: , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки:
 сходится при сходится при |
|
Пример 1
|
|
Определить, сходится или расходится ряд
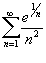 . .
Решение.
Легко видеть, что 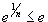 для для 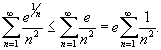 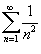 сходится как обобщенный гармонический ряд с показателем степени сходится как обобщенный гармонический ряд с показателем степени |
|
Пример 2
|
|
Определить, сходится или расходится ряд
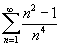 . .
Решение.
Воспользуемся признаком сравнения. Заметим, что 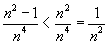 для всех натуральных n. Ряд для всех натуральных n. Ряд 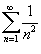 является обобщенным гармоническим рядом с является обобщенным гармоническим рядом с Таким образом, исходный ряд сходится по признаку сравнения. |
|
Пример 3
|
|
Исследовать сходимость ряда
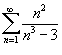 . .
Решение.
Можно заметить, что 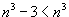 для всех натуральных n. Тогда для всех натуральных n. Тогда
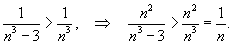 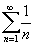 − гармонический ряд, то он расходится. Следовательно, исходный ряд также расходится по признаку сравнения. − гармонический ряд, то он расходится. Следовательно, исходный ряд также расходится по признаку сравнения. |
|
Пример 4
|
|
Определить, сходится или расходится ряд
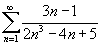 . .
Решение.
Воспользуемся предельным признаком сравнения. Будем сравнивать заданный ряд со сходящимся обобщенным гармоническим рядом 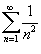 . Тогда . Тогда
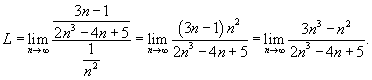 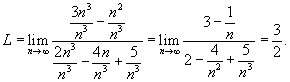 |
|
Пример 5
|
|
Исследовать ряд
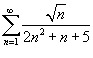 на сходимость. на сходимость.
Решение.
Будем сравнивать наш ряд со сходящимся рядом 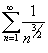 . Получаем . Получаем
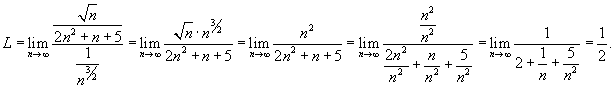 |
|
Пример 6
|
|
Исследовать ряд
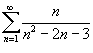 на сходимость. на сходимость.
Решение.
Применяем предельный признак сравнения. Сравним 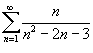 с расходящимся гармоническим рядом с расходящимся гармоническим рядом 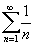 . Вычислим предел отношения соответствующих членов обоих рядов: . Вычислим предел отношения соответствующих членов обоих рядов:
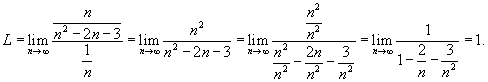 |
|
Пример 7
|
|
Определить, сходится или расходится ряд
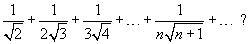
Решение.
Используем предельный признак сравнения. Будем сравнивать со сходящимся обобщенным гармоническим рядом 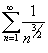 . Находим значение предела: . Находим значение предела:
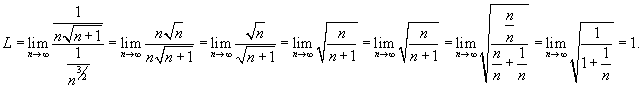 |
 , то оба ряда
, то оба ряда  , то ряд
, то ряд  , то ряд
, то ряд