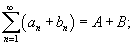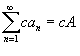|
Бесконечные ряды
|
|
Определения
Пусть задана числовая последовательность 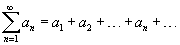 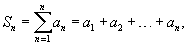  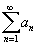 расходится. расходится.
Необходимый признак сходимости числового ряда
Если ряд 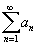 сходится, то сходится, то 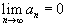 . .Внимание! Обратное утверждение неверно. Сходимость общего члена an к нулю не означает, что ряд 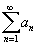 сходится. Например, гармонический ряд сходится. Например, гармонический ряд 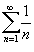 расходится, хотя расходится, хотя 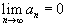 . .Соответственно, если 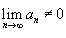 или этот предел не существует, то ряд или этот предел не существует, то ряд 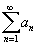 расходится (достаточное условие расходимости ряда). расходится (достаточное условие расходимости ряда).
Свойства сходящихся рядов
Предположим, что 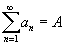 и и 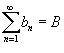 являются сходящимися рядами, а c − действительным числом. Тогда справедливы следующие линейные свойства: являются сходящимися рядами, а c − действительным числом. Тогда справедливы следующие линейные свойства:
|
|
Пример 1
|
|
Определить, сходится или расходится ряд
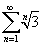 . .
Решение.
Поскольку 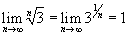 , то выполнен достаточный признак расходимости ряда. Таким образом, ряд , то выполнен достаточный признак расходимости ряда. Таким образом, ряд 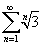 расходится. расходится. |
|
Пример 2
|
|
Исследовать сходимость ряда
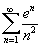 . .
Решение.
Вычислим предел 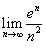 . Заменяя числовую последовательность на неперрывную функцию и применяя правило Лопиталя, получаем . Заменяя числовую последовательность на неперрывную функцию и применяя правило Лопиталя, получаем
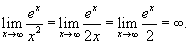 |
|
Пример 3
|
|
Показать, что гармонический ряд
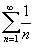 расходится. расходится.
Решение.
Запишем данный ряд в следующем виде:
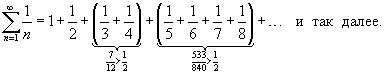 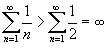 . Следовательно, гармонический ряд является расходящимся. . Следовательно, гармонический ряд является расходящимся.Этот факт впервые доказал средневековый французский экономист и математик Николь Орезм, живший более 600 лет назад. |
|
Пример 4
|
|
Исследователь сходимость ряда
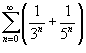 . .
Решение.
Данный ряд сходится, поскольку он является суммой двух сходящихся рядов − 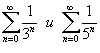 . Оба этих ряда представляют собой бесконечные геометрические прогрессии со знаменателем . Оба этих ряда представляют собой бесконечные геометрические прогрессии со знаменателем 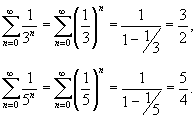 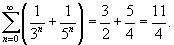 |
|
Пример 5
|
|
Исследовать сходимость ряда
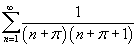 . .
Решение.
Видно, что
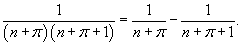 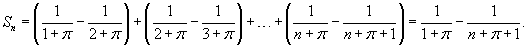 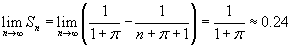 |
|
Пример 6
|
|
Определить, сходится или расходится ряд
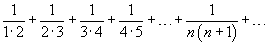 Решение. 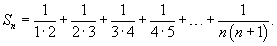 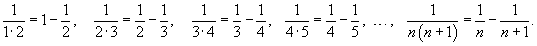 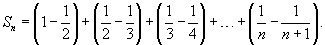 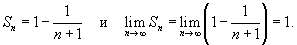 |
|
Пример 7
|
|
Исследовать сходимость ряда
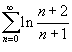 . .
Решение.
Запишем общий член ряда в виде
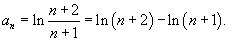 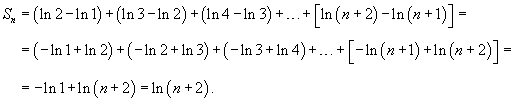 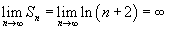 , то данный ряд расходится. , то данный ряд расходится.
|