|
Использование дифференциалов в приближенных вычислениях
|
|
Если функция y = f(x) является дифференцируемой в точке x0, то при изменении аргумента на Δx ее приращение в этой точке выражается формулой
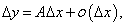 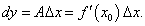 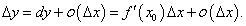 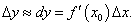 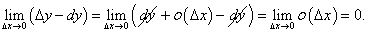 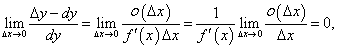 Таким образом, для приближенных расчетов можно использовать следующую формулу: 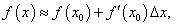 |
|
Пример 1
|
|
Найти приближенное значение
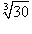 . .
Решение. 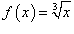 равна равна
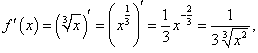 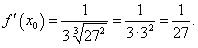 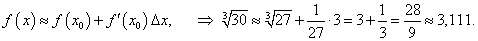 |
|
Пример 2
|
|
Вычислить приближенное значение √50.
Решение. 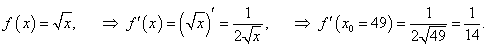 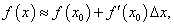 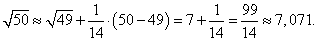 |
|
Пример 3
|
|
Вычислить приближенное значение
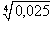 . .
Решение. 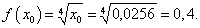 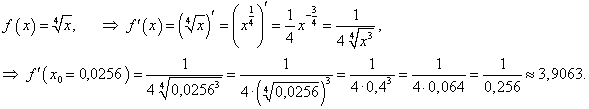 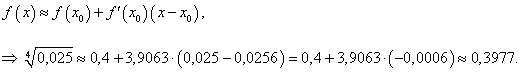 |
|
Пример 4
|
|
Вычислить (8,2)2/3.
Решение. 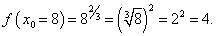 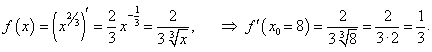 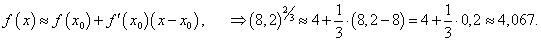 |
|
Пример 5
|
|
Вывести приближенную формулу (1 + α)n ≈ 1 + nα. Вычислить приближенное значение √1,02.
Решение. 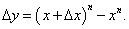 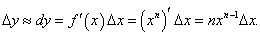 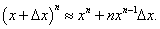 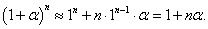 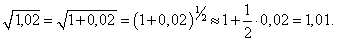 |
|
Пример 6
|
|
Вывести приближенную формулу
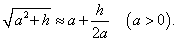 Решение. 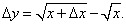  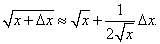 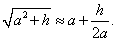 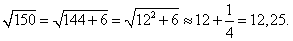 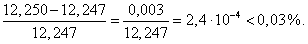 |
|
Пример 7
|
|
Вывести приближенную формулу
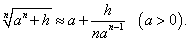 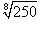 . .
Решение. 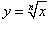 . Если переменная x получаем приращение Δx, то приращение функции имеет вид: . Если переменная x получаем приращение Δx, то приращение функции имеет вид:
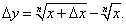 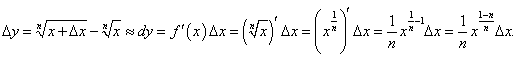  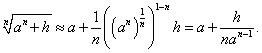 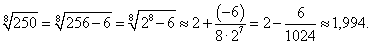 |
|
Пример 8
|
|
Найти приближенное значение cos 46°.
Решение. 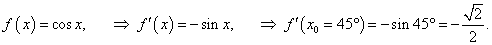 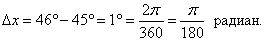 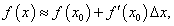 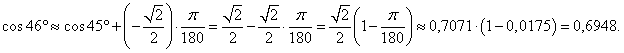 |
|
Пример 9
|
|
Найти приближенное значение sin 179°.
Решение. 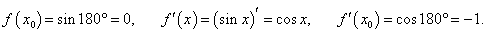 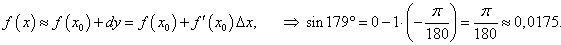 |
|
Пример 10
|
|
Найти приближенное значение ln 20.
Решение. 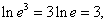 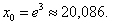 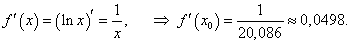 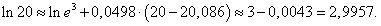 |
|
Пример 11
|
|
Вычислить e0,1.
Решение. 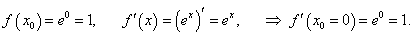 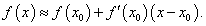 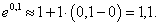 |
|
Пример 12
|
|
Найти приближенное значение arccos 0,51.
Решение. 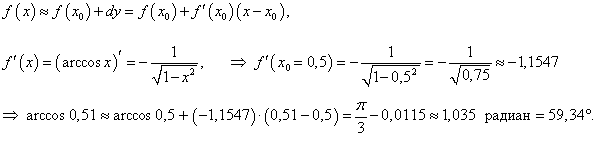 |
|
Пример 13
|
|
Найти приближенное значение arctan 0,95.
Решение. 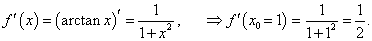 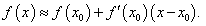 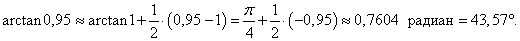 |
|
Пример 14
|
|
Найти приближенное значение функции
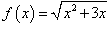 при x = 1,02. при x = 1,02.
Решение. 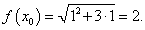 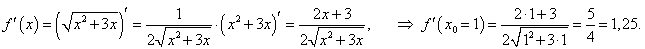 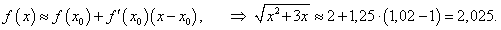 |
|
Пример 15
|
|
Найти приближенное значение функции f(x) = √5x − 1 при x = 1,99.
Решение. 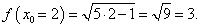 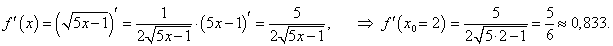 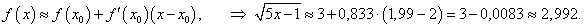 |