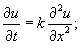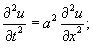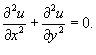|
Решение дифференциальных уравнений с помощью рядов Фурье
|
||||||
|
Теория рядов Фурье первоначально была создана для решения дифференциальных уравнений. Поэтому, неудивительно, что ряды Фурье широко используются для поиска решений как обыкновенных дифференциальных уравнений, так и уравнений в частных производных.
В настоящем разделе мы расмотрим приложение рядов Фурье к решению некоторых обыкновенных дифференциальных уравнений, а также к решению трех наиболее популярных типов уравнений математической физики:
|
||||||
|
Пример 1
|
||||||
|
Найти решение в виде ряда Фурье дифференциального уравнения
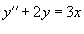 с граничными условиями с граничными условиями 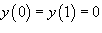 . .
Решение. 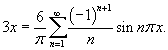 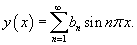 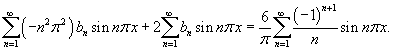 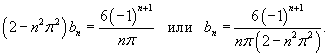 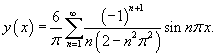 |
||||||
|
Пример 2
|
||||||
|
Найти периодические решения дифференциального уравнения
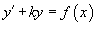 , где , где Решение. 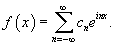 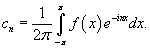 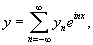 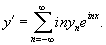 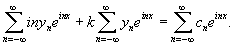 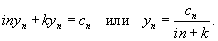 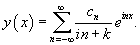 |
||||||
|
Пример 3
|
||||||
|
Используя разложение в ряд Фурье, решить одномерное уравнение теплопроводности
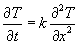 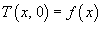 . .
Решение. Рассмотрим уравнение 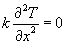 . Интегрируя его, найдем общее решение: . Интегрируя его, найдем общее решение:
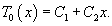 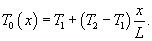 Введем новую переменную 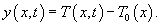 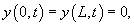 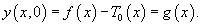 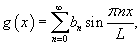 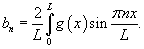 Общее решение будем искать в виде ряда с коэффициентами 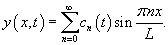 Начальные условия для 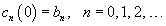 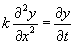 . Тогда . Тогда
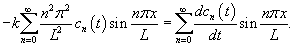 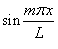 и проинтегрируем на интервале и проинтегрируем на интервале 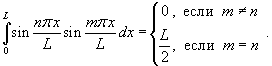 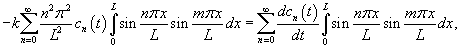 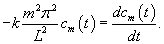 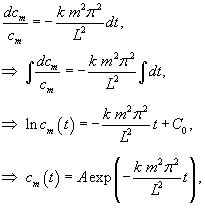 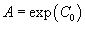 − постоянная, зависящая от начальных условий. − постоянная, зависящая от начальных условий.Учитывая, что 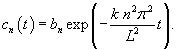 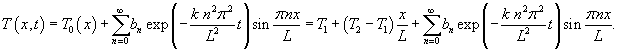 |
||||||
|
Пример 4
|
||||||
|
Найти решение волнового уравнения
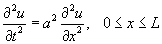 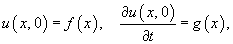 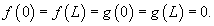 Решение. 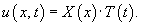 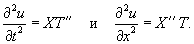 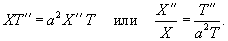 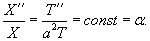 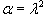 , получим уравнение , получим уравнение
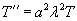 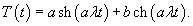 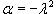 . В этом случае волновое уравнение расщепляется на два обыкновенных дифференциальных уравнения: . В этом случае волновое уравнение расщепляется на два обыкновенных дифференциальных уравнения:
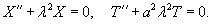 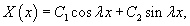 Учитывая граничные условия, получаем 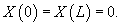 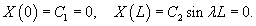 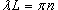 (n − целое число). (n − целое число).Следовательно, так называемые собственные значения равны 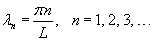 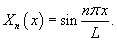 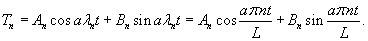 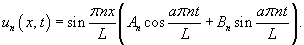 Теперь мы можем построить общее решение волнового уравнения как линейную комбинацию частных решений: 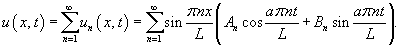 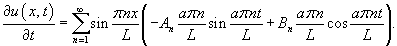 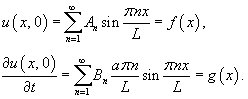  . По формулам для коэффициентов Фурье получаем . По формулам для коэффициентов Фурье получаем
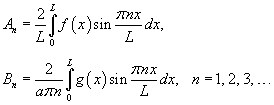 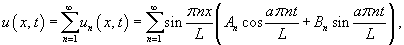 Первый член ряда 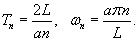 |
||||||
|
Пример 5
|
||||||
|
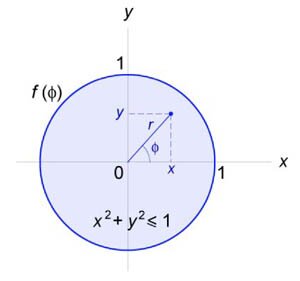
Найти решение уравнения Лапласа
 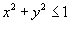 c граничным условием c граничным условием
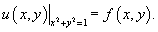 Решение. 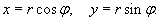
Уравнение Лапласа в полярных координатах записывается в виде 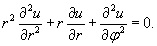 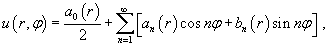 Предполагая, что функция 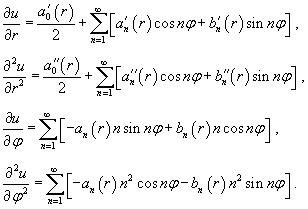 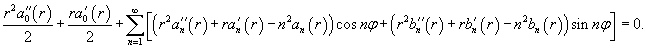 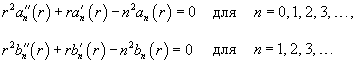 Убедимся, что полученным уравнениям удовлетворяют функции вида 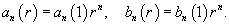 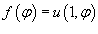 , определяющую граничные условия для уравнения Лапласа в полярных координатах. В результате находим , определяющую граничные условия для уравнения Лапласа в полярных координатах. В результате находим
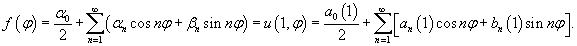 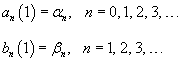 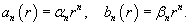 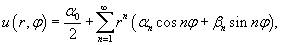 Полученный ответ можно упростить. Подставим явные выражения для коэффициентов αn, βn: 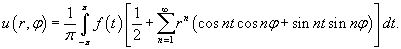 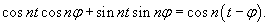 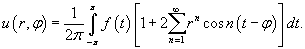 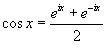 , можно показать, что выражение в квадратных скобках равно сумме бесконечно убывающей геометрической прогрессии: , можно показать, что выражение в квадратных скобках равно сумме бесконечно убывающей геометрической прогрессии:
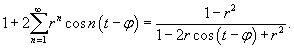 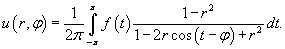 |
||||||