|
Моделирование рекламной кампании
|
||||||||||||
|
Дифференциальные уравнения широко используются для описания различных динамических процессов в экономике, логистике и маркетинге. Ниже мы рассмотрим как с помощью обыкновенных дифференциальных уравнений можно смоделировать рекламную кампанию.
Представим, что некоторая компания разработала новый продукт или сервис. Маркетинговая стратегия компании предполагает агрессивное рекламирование. Чтобы перейти к простой математической модели, введем две переменных:
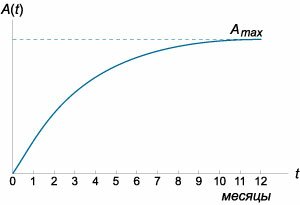
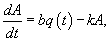 Данное уравнение содержит два члена в правой части. Первое слагаемое Мы можем принять в первом приближении, что скорость забывания пропорциональна текущему уровню осведомленности A. Полученное уравнение является линейным дифференциальным уравнением первого порядка. Его удобнее записать в стандартной форме: 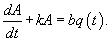 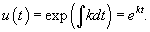 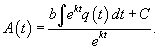 В приведенных ниже примерах мы исследуем как осведомленность потребителей |
||||||||||||
|
Пример 1
|
||||||||||||
|
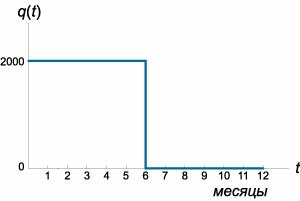
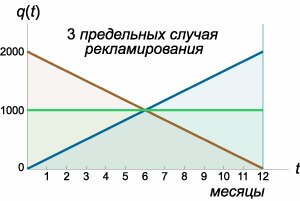
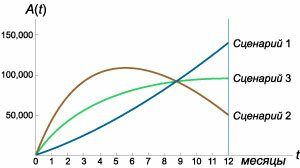
Менеджмент компании принял решение о постоянном рекламировании нового продукта в течение года. Рекламный бюджет составляет
Решение. 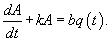 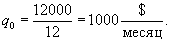 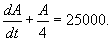 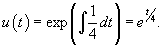 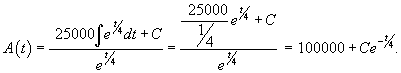 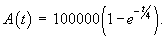 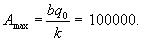 |
||||||||||||
|
Пример 2
|
||||||||||||
|
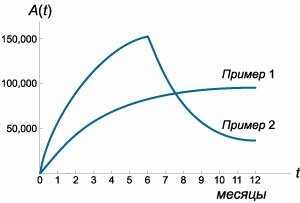
Используя условия предыдущей задачи 1, выяснить как изменится число потенциальных покупателей к концу года, если весь рекламный бюджет израсходовать равномерно в течение первых 6 месяцев?
Решение. Задача разбивается на две стадии. К концу 6-го месяца величина A легко вычисляется по формуле 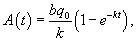 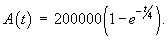 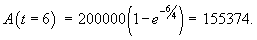 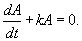 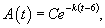  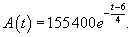 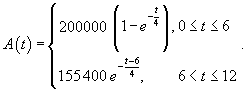
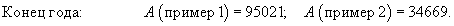 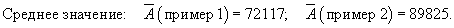 |
||||||||||||
|
Пример 3
|
||||||||||||
|
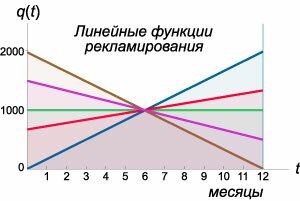
Исследовать динамику осведомленности
Решение. 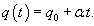
Ясно, что параметры q0 и α будут связаны следующим соотношением: 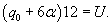 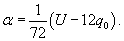 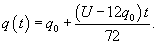 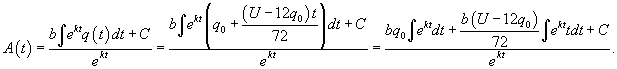 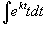 в числителе можно найти, интегрируя по частям. Полагаем: в числителе можно найти, интегрируя по частям. Полагаем:
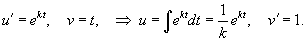 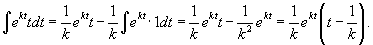 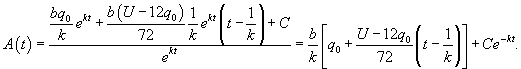 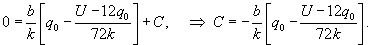 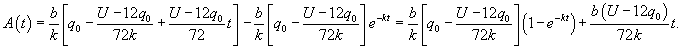 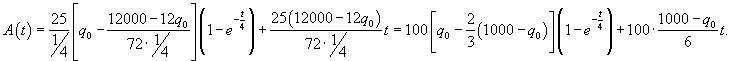 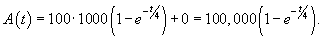
|
||||||||||||