Определение ряда Фурье и типичные примеры

Говорят, что функция \(f\left( x \right)\) имеет период \(P,\) если \(f\left( {x + P} \right) = f\left( x \right)\) для всех значений \(x.\) Пусть период функции \(f\left( x \right)\) равен \(2\pi.\) В этом случае достаточно рассмотреть поведение функции в интервале \(\left[ { - \pi ,\pi } \right].\)

1. Предположим, что функция \(f\left( x \right)\) с периодом \(2\pi\) абсолютно интегрируема в интервале \(\left[ { - \pi ,\pi } \right].\) При этом является конечным так называемый интеграл Дирихле: \[\int\limits_{ - \pi }^\pi {\left| {f\left( x \right)} \right|dx} < \infty ;\]

2. Предположим также, что функция \(f\left( x \right)\) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).

Если условия \(1\) и \(2\) выполнены, то ряд Фурье для функции \(f\left( x \right)\) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье).

Если \({x_0}\) − точка разрыва, то ряд Фурье сходится к значению \[\lim\limits_{\varepsilon \to 0} \frac{1}{2}\left[ {f\left( {{x_0} - \varepsilon } \right) - f\left( {{x_0} + \varepsilon } \right)} \right].\] Ряд Фурье функции \(f\left( x \right)\) представляется в виде \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left\{ {{a_n}\cos nx + {b_n}\sin nx} \right\}} ,\] где коэффициенты Фурье \({{a_0}},\) \({{a_n}}\) и \({{b_n}}\) определяются формулами \[ {{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)dx} ,}\;\; {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nx dx} ,}\;\; {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nx dx} .} \] Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя \({{a_n}}\) и \({{b_n}}\) новыми переменными \({{d_n}}\) и \({{\varphi_n}}\) или \({{d_n}}\) и \({{\theta_n}},\) где \[ {{d_n} = \sqrt {a_n^2 + b_n^2} ,}\;\; {\tan {\varphi _n} = \frac{{{a_n}}}{{{b_n}}},}\;\; {\tan {\theta _n} = \frac{{{b_n}}}{{{a_n}}},} \] можно, соответственно, записать \[ {f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{d_n}\sin \left( {nx + {\varphi _n}} \right)} \;\;\text{или}\;\;} {f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{d_n}\cos\left( {nx + {\theta _n}} \right)} .} \] Разложение в ряд Фурье четной функции \(f\left( x \right)\) с периодом \(2\pi\) не содержит синусов и имеет вид \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos nx} ,\] где коэффициенты Фурье определяются выражениями \[ {{a_0} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)dx} ,}\;\; {{a_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\cos nxdx} .} \] Аналогично, разложение в ряд Фурье нечетной функции \(f\left( x \right),\) имеющей период \(2\pi,\) содержит только синусы и имеет вид \[f\left( x \right) = \sum\limits_{n = 1}^\infty {{b_n}\sin nx} ,\] где коэффициенты \({{b_n}}\) равны \[{b_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\sin nxdx} .\] Ниже мы рассмотрим некоторые типичные примеры разложения функций с периодом \(2\pi\) в ряд Фурье, предполагая, что такие разложения существуют и сходятся к заданной функции.

   Пример 1

Пусть функция \(f\left( x \right)\) имеет период \(2\pi\) и раскладывается в ряд Фурье: \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left\{ {{a_n}\cos nx + {b_n}\sin nx} \right\}} .\] Вычислить коэффициенты \({{a_0}},\) \({{a_n}}\) и \({{b_n}}.\) Чтобы найти \({{a_0}},\) проинтегрируем ряд Фурье в интервале \(\left[ { - \pi ,\pi } \right]:\) \[ {\int\limits_{ - \pi }^\pi {f\left( x \right)dx} } = {\pi {a_0} + \sum\limits_{n = 1}^\infty {\left[ {{a_n}\int\limits_{ - \pi }^\pi {\cos nxdx} + {b_n}\int\limits_{ - \pi }^\pi {\sin nxdx} } \right]} .} \] Для всех \(n > 0\) справедливо \[ {\int\limits_{ - \pi }^\pi {\cos nxdx} = \left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_{ - \pi }^\pi = 0\;\;\text{и}\;\;} {\int\limits_{ - \pi }^\pi {\sin nxdx} = \left. {\left( { - \frac{{\cos nx}}{n}} \right)} \right|_{ - \pi }^\pi = 0.} \] Поэтому, все члены в разложении Фурье справа от знака суммы равны нулю, что приводит к соотношению \[ {\int\limits_{ - \pi }^\pi {f\left( x \right)dx} = \pi {a_0}\;\;\text{или}\;\;} {{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)dx} .} \] Чтобы определить коэффициенты \({{a_n}},\) умножим обе части разложения в ряд Фурье на \(\cos mx\) и проинтегрируем почленно: \[ {\int\limits_{ - \pi }^\pi {f\left( x \right)\cos mxdx} } = {\frac{{{a_0}}}{2}\int\limits_{ - \pi }^\pi {\cos mxdx} } + {\sum\limits_{n = 1}^\infty {\left[ {{a_n}\int\limits_{ - \pi }^\pi {\cos nx\cos mxdx} + {b_n}\int\limits_{ - \pi }^\pi {\sin nx\cos mxdx} } \right]} .} \] Первое слагаемое в правой части равно нулю. Тогда, используя тригонометрические тождества, можно записать \[ {\int\limits_{ - \pi }^\pi {\sin nx\cos mxdx} } = {\frac{1}{2}\int\limits_{ - \pi }^\pi {\left[ {\sin\left( {n + m} \right)x + \sin \left( {n - m} \right)x} \right]dx} = 0,} \] \[ {\int\limits_{ - \pi }^\pi {\cos nx\cos mxdx} } = {\frac{1}{2}\int\limits_{ - \pi }^\pi {\left[ {\cos \left( {n + m} \right)x + \cos \left( {n - m} \right)x} \right]dx} = 0,} \] если \(m \ne n.\)

В случае \(m = n\) получаем \[\require{cancel} {\int\limits_{ - \pi }^\pi {\sin nx\cos mxdx} } = {\frac{1}{2}\int\limits_{ - \pi }^\pi {\left[ {\sin 2mx + \sin 0} \right]dx} ,}\;\; {\Rightarrow \int\limits_{ - \pi }^\pi {{\sin^2}mxdx} = \frac{1}{2}\left[ {\left. {\left( { - \frac{{\cos 2mx}}{{2m}}} \right)} \right|_{ - \pi }^\pi } \right] } = {\frac{1}{{4m}}\left[ { - \cancel{\cos \left( {2m\pi } \right)} + \cancel{\cos \left( {2m\left( { - \pi } \right)} \right)}} \right] = 0;} \] \[ {\int\limits_{ - \pi }^\pi {\cos nx\cos mxdx} } = {\frac{1}{2}\int\limits_{ - \pi }^\pi {\left[ {\cos 2mx + \cos 0} \right]dx} ,}\;\; {\Rightarrow \int\limits_{ - \pi }^\pi {{\cos^2}mxdx} } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{\sin 2mx}}{{2m}}} \right)} \right|_{ - \pi }^\pi + 2\pi } \right] } = {\frac{1}{{4m}}\left[ {\sin \left( {2m\pi } \right) - \sin \left( {2m\left( { - \pi } \right)} \right)} \right] + \pi = \pi .} \] Таким образом, \[ {\int\limits_{ - \pi }^\pi {f\left( x \right)\cos mxdx} = {a_m}\pi ,}\;\; {\Rightarrow {a_m} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos mxdx} ,}\;\; {m = 1,2,3, \ldots } \] Аналогично, умножая ряд Фурье на \(\sin mx\) и интегрируя почленно, получим выражение для \({{b_m}}:\) \[ {{b_m} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin mxdx} ,}\;\; {m = 1,2,3, \ldots } \] Переписывая формулы для \({{a_n}},\) \({{b_n}},\) запишем окончательные выражения для коэффициентов Фурье: \[ {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nxdx} ,}\;\; {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nxdx} .} \]

   Пример 2

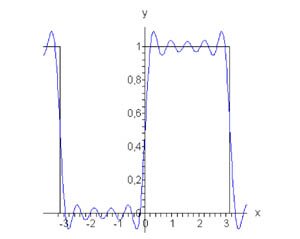
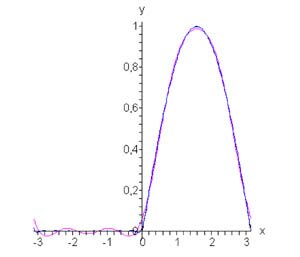
Найти разложение в ряд Фурье прямоугольной функции с периодом \(2\pi,\) определенной в интервале \(\left[ { - \pi ,\pi } \right]:\) \[ f\left( x \right) = \begin{cases} 0, & \text{если} & - \pi \le x \le 0 \\ 1, & \text{если} & 0 < x \le \pi \end{cases}. \] Вычислим сначала \({{a_0}}:\) \[ {{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)dx} } = {\frac{1}{\pi }\int\limits_0^\pi {1dx} } = {\frac{1}{\pi } \cdot \pi = 1.} \] Определим теперь коэффициенты Фурье при \(n \ne 0:\) \[ {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nxdx} } = {\frac{1}{\pi }\int\limits_0^\pi {1 \cdot \cos nxdx} } = {\frac{1}{\pi }\left[ {\left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_0^\pi } \right] } = {\frac{1}{{\pi n}} \cdot 0 = 0,} \] \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nxdx} } = {\frac{1}{\pi }\int\limits_0^\pi {1 \cdot \sin nxdx} } = {\frac{1}{\pi }\left[ {\left. {\left( { - \frac{{\cos nx}}{n}} \right)} \right|_0^\pi } \right] } = { - \frac{1}{{\pi n}} \cdot \left( {\cos n\pi - \cos 0} \right) } = {\frac{{1 - \cos n\pi }}{{\pi n}}.} \] Поскольку \(\cos n\pi = {\left( { - 1} \right)^n},\) то можно записать \[{b_n} = \frac{{1 - {{\left( { - 1} \right)}^n}}}{{\pi n}}.\] Таким образом, разложение в ряд Фурье для прямоугольной функции имеет вид \[f\left( x \right) = \frac{1}{2} + \sum\limits_{n = 1}^\infty {\frac{{1 - {{\left( { - 1} \right)}^n}}}{{\pi n}}\sin nx} .\] Можно легко вычислить несколько первых членов разложения. Полагая, например, \(n = 5,\) получаем \[ {f\left( x \right) = \frac{1}{2} + \frac{{1 - \left( { - 1} \right)}}{\pi }\sin x } + {\frac{{1 - {{\left( { - 1} \right)}^2}}}{{2\pi }}\sin 2x } + {\frac{{1 - {{\left( { - 1} \right)}^3}}}{{3\pi }}\sin 3x } + {\frac{{1 - {{\left( { - 1} \right)}^4}}}{{4\pi }}\sin 4x } + {\frac{{1 - {{\left( { - 1} \right)}^5}}}{{5\pi }}\sin 5x + \ldots } = {\frac{1}{2} + \frac{2}{\pi }\sin x } + {\frac{2}{{3\pi }}\sin 3x } + {\frac{2}{{5\pi }}\sin 5x + \ldots } \] На рисунке \(1\) представлены график данной функции и ее аппроксимация рядом Фурье при \(n = 10.\)

   Пример 3

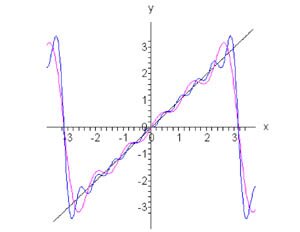
Найти разложение в ряд Фурье для пилообразной функции, определенной в интервале \(\left[ { - \pi ,\pi } \right]\) и имеющей период \(2\pi.\) Определим коэффициенты Фурье для пилообразной волны.
Поскольку функция нечетная (рисунок \(2\)), то \({a_0} = {a_n} = 0.\) \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nxdx} } = {\frac{1}{\pi }\int\limits_{ - \pi }^\pi {x\sin nxdx} .} \] Для вычисления последнего интеграла используем формулу интегрирования по частям: \[\int\limits_{ - \pi }^\pi {udv} = \left. {\left( {uv} \right)} \right|_{ - \pi }^\pi - \int\limits_{ - \pi }^\pi {vdu} .\] Пусть \(u = x,\;dv = \sin nxdx.\) Тогда \(du = dx,\;v = \int {\sin nxdx} = - \large\frac{{\cos nx}}{n}\normalsize,\) и интеграл будет равен \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {x\sin nxdx} } = {\frac{1}{\pi }\left[ {\left. {\left( { - \frac{{\cos nx}}{n}} \right)} \right|_{ - \pi }^\pi - \int\limits_{ - \pi }^\pi {\left( { - \frac{{\cos nx}}{n}} \right)dx} } \right] } = {\frac{1}{\pi }\left[ {\left( { - \frac{{\pi \cos n\pi }}{n} + \frac{{\left( { - \pi } \right)\cos \left( { - n\pi } \right)}}{n}} \right) + \frac{1}{n}\int\limits_{ - \pi }^\pi {\cos nxdx} } \right] } = {\frac{1}{{n\pi }}\left[ { - 2\pi \cos n\pi + \left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_{ - \pi }^\pi } \right] } = {\frac{1}{{n\pi }}\left[ { - 2\pi \cos n\pi + \frac{1}{n}\left( {\sin n\pi - \sin \left( { - n\pi } \right)} \right)} \right] } = {\frac{1}{{n\pi }}\left[ { - 2\pi \cos n\pi + \frac{{2\sin n\pi }}{n}} \right] } = {\frac{2}{{n\pi }}\left[ {\frac{{\sin n\pi }}{n} - \pi \cos n\pi } \right].} \] Подставляя \(\sin n\pi = 0\) и \(\cos n\pi = {\left( { - 1} \right)^n}\) для всех натуральных значений \(n,\) получаем \[ {{b_n} = \frac{2}{{n\pi }}\left( { - \pi {{\left( { - 1} \right)}^n}} \right) } = { - \frac{2}{n}{\left( { - 1} \right)^n} } = {\frac{2}{n}{\left( { - 1} \right)^{n + 1}}.} \] Следовательно, разложение в ряд Фурье прилообразной волны имеет вид (рисунок \(2\) выше) \[x = \sum\limits_{n = 1}^\infty {\frac{2}{n}{{\left( { - 1} \right)}^{n + 1}}\sin nx} .\]

   Пример 4

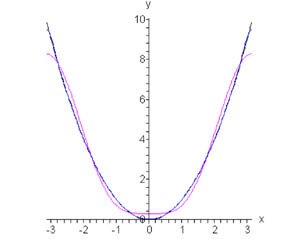
Предположим, что \(f\left( x \right)\) является периодической функцией с периодом \(2\pi.\) Пусть \(f\left( x \right) = {x^2}\) для \(x \in \left[ { - \pi ,\pi } \right].\) Найти разложение Фурье для заданной параболической функции. Так как функция четная, то коэффициенты \({b_n} = 0.\) Тогда \[ {{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)dx} } = {\frac{1}{\pi }\int\limits_{ - \pi }^\pi {{x^2}dx} = \frac{2}{\pi }\int\limits_0^\pi {{x^2}dx} } = {\frac{2}{\pi } \cdot \left[ {\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^\pi } \right] } = {\frac{2}{\pi } \cdot \frac{{{\pi ^3}}}{3} } = {\frac{{2{\pi ^2}}}{3},} \] \[ {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nxdx} } = {\frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\cos nxdx} } = {\frac{2}{\pi }\int\limits_0^\pi {{x^2}\cos nxdx} .} \] Применим дважды интегрирование по частям. \[ {{a_n} = \frac{2}{\pi }\int\limits_0^\pi {{x^2}\cos nxdx} } = {\left[ {\begin{array}{*{20}{l}} {u = {x^2}}\\ {dv = \cos nxdx}\\ {du = 2xdx}\\ {v = \int {\cos nxdx} = \frac{{\sin nx}}{n}} \end{array}} \right] } = {\frac{2}{\pi }\left[ {\left. {\left( {\frac{{{x^2}\sin nx}}{n}} \right)} \right|_0^\pi - \int\limits_0^\pi {2x\frac{{\sin nx}}{n}dx} } \right] } = {\frac{2}{{\pi n}}\left[ {{\pi ^2}\sin n\pi - {{\left( { - \pi } \right)}^2}\sin \left( { - n\pi } \right) - 2\int\limits_0^\pi {x\sin nxdx} } \right] } = {\frac{2}{{\pi n}}\left[ {2{\pi ^2}\sin n\pi - 2\int\limits_0^\pi {x\sin nxdx} } \right] } = { - \frac{4}{{\pi n}}\int\limits_0^\pi {x\sin nxdx} } = {\left[ {\begin{array}{*{20}{l}} {u = x}\\ {dv = \sin nxdx}\\ {du = dx}\\ {v = \int {\sin nxdx} = - \frac{{\cos nx}}{n}} \end{array}} \right] } = { - \frac{4}{{\pi n}}\left[ {\left. {\left( { - \frac{{x\cos nx}}{n}} \right)} \right|_0^\pi - \int\limits_0^\pi {\left( { - \frac{{\cos nx}}{n}} \right)dx} } \right] } = {\frac{4}{{\pi {n^2}}}\left[ {\pi \cos n\pi - \int\limits_0^\pi {\cos nxdx} } \right] } = {\frac{4}{{\pi {n^2}}}\left[ {\pi \cos n\pi - \left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_0^\pi } \right] } = {\frac{4}{{\pi {n^2}}}\left[ {\pi \cos n\pi - \frac{{\sin n\pi }}{n}} \right].} \] Поскольку \(\sin n\pi = 0\) и \(\cos n\pi = {\left( { - 1} \right)^n}\) для натуральных \(n,\) то получаем \[ {{a_n} = \frac{4}{{\pi {n^2}}} \cdot \pi {\left( { - 1} \right)^n} } = {\frac{4}{{{n^2}}}{\left( { - 1} \right)^n}.} \] Тогда разложение параболической функции в ряд Фурье имеет вид (рисунок \(3\)) \[{x^2} = \frac{{{\pi ^2}}}{3} + \sum\limits_{n = 1}^\infty {\frac{4}{{{n^2}}}{{\left( { - 1} \right)}^n}\cos nx} .\]

   Пример 5

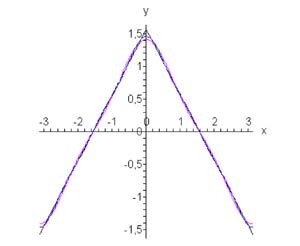
Найти ряд Фурье для треугольной волны \[ f\left( x \right) = \begin{cases} \frac{\pi }{2} + x, & \text{если} & - \pi \le x \le 0 \\ \frac{\pi }{2} - x, & \text{если} & 0 < x \le \pi \end{cases}, \] определенной в интервале \(\left[ { - \pi ,\pi } \right].\) Постоянная \({a_0}\) равна \[ {{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)dx} } = {\frac{1}{\pi }\left[ {\int\limits_{ - \pi }^0 {\left( {\frac{\pi }{2} + x} \right)dx} + \int\limits_0^\pi {\left( {\frac{\pi }{2} - x} \right)dx} } \right] } = {\frac{1}{\pi }\left[ {\left. {\left( {\frac{\pi }{2}x + \frac{{{x^2}}}{2}} \right)} \right|_{ - \pi }^0 + \left. {\left( {\frac{\pi }{2}x - \frac{{{x^2}}}{2}} \right)} \right|_0^\pi } \right] } = {\frac{1}{\pi }\left[ {0 - \left( { - \cancel{\frac{{{\pi ^2}}}{2}} + \cancel{\frac{{{{\left( { - \pi } \right)}^2}}}{2}}} \right) + \left( {\cancel{\frac{{{\pi ^2}}}{2}} - \cancel{\frac{{{\pi ^2}}}{2}}} \right) - 0} \right] = 0.} \] Вычислим коэффициенты \({a_n}:\) \[ {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nxdx} } = {\frac{1}{\pi }\left[ {\int\limits_{ - \pi }^0 {\left( {\frac{\pi }{2} + x} \right)\cos nxdx} + \int\limits_0^\pi {\left( {\frac{\pi }{2} - x} \right)\cos nxdx} } \right] } = {\frac{1}{\pi }\left[ {\int\limits_{ - \pi }^0 {\frac{\pi }{2}\cos nxdx} + \int\limits_{ - \pi }^0 {x\cos nxdx} } \right. } + {\left. {\int\limits_0^\pi {\frac{\pi }{2}\cos nxdx} - \int\limits_0^\pi {x\cos nxdx} } \right].} \] Интегрируя по частям, можно записать \[ {\int {x\cos nxdx} = \frac{{x\sin nx}}{n} - \int {\frac{{x\sin nx}}{n}dx} } = {\frac{{x\sin nx}}{n} + \frac{{\cos nx}}{{{n^2}}}.} \] Тогда \[ {{a_n} = \frac{1}{\pi }\left[ {\frac{\pi }{2}\left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_{ - \pi }^0 + \left. {\left( {\frac{{x\sin nx}}{n} + \frac{{\cos nx}}{{{n^2}}}} \right)} \right|_{ - \pi }^0} \right. } + {\;\left. {\frac{\pi }{2}\left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_0^\pi - \left. {\left( {\frac{{x\sin nx}}{n} + \frac{{\cos nx}}{{{n^2}}}} \right)} \right|_0^\pi } \right].} \] Значения \(\sin nx\) при \(x = 0\) или \(x = \pm \pi\) равны нулю. Поэтому \[ {{a_n} = \frac{1}{{\pi {n^2}}}\left[ {\left. {\left( {\cos nx} \right)} \right|_{ - \pi }^0 - \left. {\left( {\cos nx} \right)} \right|_0^\pi } \right] } = {\frac{1}{{\pi {n^2}}}\left[ {\cos 0 - \cos \left( { - \pi n} \right) - \cos \pi n + \cos 0} \right] } = {\frac{2}{{\pi {n^2}}}\left[ {1 - \cos \pi n} \right] } = {\frac{2}{{\pi {n^2}}}\left[ {1 - {{\left( { - 1} \right)}^n}} \right].} \] Если \(n = 2k,\) то \({a_{2k}} = 0.\) Если \(n = 2k + 1,\) то \({a_{2k + 1}} = \large\frac{4}{{\pi {n^2}}}\normalsize,\;k = 0,1,2,3, \ldots \)
Так как функция \(f\left( x \right)\) четная, то коэффициенты Фурье \({b_n}\) равны нулю. Таким образом, окончательное разложение треугольной волны в ряд Фурье выглядит следующим образом (см. рис. \(4\)): \[f\left( x \right) = \frac{4}{\pi }\sum\limits_{k = 0}^\infty {\frac{{\cos \left( {2k + 1} \right)x}}{{{{\left( {2k + 1} \right)}^2}}}} .\]

   Пример 6

Найти разложение в ряд Фурье для функции \[ f\left( x \right) = \begin{cases} 0, & \text{если} & - \pi \le x \le 0 \\ \sin x, & \text{если} & 0 < x \le \pi \end{cases}, \] заданной в интервале \(\left[ { - \pi ,\pi } \right].\) Найдем сначала \({a_0}:\) \[ {{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)dx} } = {\frac{1}{\pi }\int\limits_0^\pi {\sin xdx} } = {\frac{1}{\pi }\left[ {\left. {\left( { - \cos x} \right)} \right|_0^\pi } \right] } = {\frac{1}{\pi }\left( { - \cos \pi + \cos 0} \right) } = {\frac{2}{\pi }.} \] Далее вычислим коэффициенты \({a_n}:\) \[ {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nxdx} } = {\frac{1}{\pi }\int\limits_0^\pi {\sin x\cos nxdx} } = {\frac{1}{{2\pi }}\int\limits_0^\pi {\left[ {\sin \left( {x + nx} \right) + \sin\left( {x - nx} \right)} \right]dx} } = {\frac{1}{{2\pi }}\int\limits_0^\pi {\left[ {\sin \left( {n + 1} \right)x + \sin\left( {n - 1} \right)x} \right]dx} } = {\frac{1}{{2\pi }}\left[ {\left. {\left( { - \frac{{\cos \left( {n + 1} \right)x}}{{n + 1}} + \frac{{\cos \left( {n - 1} \right)x}}{{n - 1}}} \right)} \right|_0^\pi } \right] } = {\frac{1}{{2\pi }}\left[ {\frac{{\cos \left( {n - 1} \right)\pi }}{{n - 1}} - \frac{{\cos \left( {n + 1} \right)\pi }}{{n + 1}} - \frac{1}{{n - 1}} + \frac{1}{{n + 1}}} \right] } = {\frac{1}{{2\pi }}\left[ {\frac{{\cos \left( {n - 1} \right)\pi }}{{n - 1}} - \frac{{\cos \left( {n + 1} \right)\pi }}{{n + 1}} - \frac{2}{{{n^2} - 1}}} \right].} \] Заметим, что \[ {\cos \left( {n + 1} \right)\pi } = {\cos \left( {\pi n + \pi } \right) } = {\cos \left( {\pi n - \pi + 2\pi } \right) } = {\cos \left( {\left( {n - 1} \right)\pi + 2\pi } \right) } = {\cos \left( {n - 1} \right)\pi .} \] Поскольку \(\cos \left( {n - 1} \right)\pi = {\left( { - 1} \right)^{n - 1}},\) то для коэффициентов \({a_n}\) получаем выражение \[{a_n} = \frac{1}{{2\pi }} \cdot \frac{2}{{{n^2} - 1}} \cdot \left[ {{{\left( { - 1} \right)}^{n - 1}} - 1} \right].\] Видно, что \({a_n} = 0\) для нечетных \(n.\) Для четных \(n,\) когда \(n = 2k\;\left( {k = 1,2,3, \ldots } \right),\) мы имеем \[{a_{2k}} = \frac{1}{{2\pi }} \cdot \left( { - \frac{4}{{{k^2} - 1}}} \right) = - \frac{1}{\pi } \cdot \frac{2}{{{k^2} - 1}}.\] Вычислим теперь коэффициенты \({b_n}.\) Начнем с \({b_1}:\) \[ {{b_1} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin xdx} } = {\frac{1}{\pi }\int\limits_0^\pi {\sin x\sin xdx} } = {\frac{1}{\pi }\int\limits_0^\pi {{{\sin }^2}xdx} } = {\frac{1}{{2\pi }}\int\limits_0^\pi {\left( {1 - \cos 2x} \right)dx} } = {\frac{1}{{2\pi }}\left[ {\left. {\left( {x - \frac{{\sin 2x}}{2}} \right)} \right|_0^\pi } \right] } = {\frac{1}{{2\pi }} \cdot \pi = \frac{1}{2}.} \] Остальные коэффициенты \({b_n}\) при \(n > 1\) равны нулю. Действительно, \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nxdx} } = {\frac{1}{\pi }\int\limits_0^\pi {\sin x\sin nxdx} } = {\frac{1}{{2\pi }}\int\limits_0^\pi {\left[ {\cos \left( {x - nx} \right) - \cos \left( {x + nx} \right)} \right]dx} } = {\frac{1}{{2\pi }}\int\limits_0^\pi {\left[ {\cos \left( {n - 1} \right)x - \cos \left( {n + 1} \right)x} \right]dx} } = {\frac{1}{{2\pi }}\left[ {\left. {\left( {\frac{{\sin \left( {n - 1} \right)x}}{{n - 1}} - \frac{{\sin \left( {n + 1} \right)x}}{{n + 1}}} \right)} \right|_0^\pi } \right] = 0} \] Таким образом, формула разложения заданной функции в ряд Фурье имеет вид \[ {f\left( x \right) = \frac{1}{\pi } + \frac{1}{2}\sin x } - {\frac{2}{\pi }\sum\limits_{k = 1}^\infty {\frac{1}{{4{k^2} - 1}}\cos \left( {2kx} \right)} .} \] График функции и варианты разложения для \(n = 2\) и \(n = 8\) показаны на рисунке \(5.\)

   Пример 7

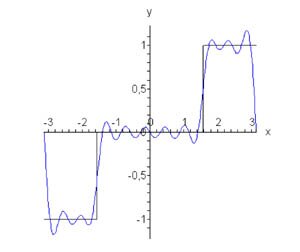
Найти ряд Фурье для функции \[ f\left( x \right) = \begin{cases} -1, & \text{если} & - \pi \le x \le - \frac{\pi }{2} \\ 0, & \text{если} & - \frac{\pi }{2} \lt x \le \frac{\pi }{2} \\ 1, & \text{если} & \frac{\pi }{2} < x \le \pi \end{cases}, \] определенной в интервале \(\left[ { - \pi ,\pi } \right].\) \[ {{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)dx} } = {\frac{1}{\pi }\left[ {\int\limits_{ - \pi }^{ - \large\frac{\pi }{2}\normalsize} {\left( { - 1} \right)dx} + \int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {0dx} + \int\limits_{\large\frac{\pi }{2}\normalsize}^\pi {1dx} } \right] } = {\frac{1}{\pi }\left( { - \cancel{\frac{\pi }{2}} + 0 + \cancel{\frac{\pi }{2}}} \right) = 0.} \] Вычислим коэффициенты \({a_n}:\) \[ {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nxdx} } = {\frac{1}{\pi }\left[ {\int\limits_{ - \pi }^{ - \large\frac{\pi }{2}\normalsize} {\left( { - \cos nx} \right)dx} + \int\limits_{\large\frac{\pi }{2}\normalsize}^\pi {\cos nxdx} } \right] } = {\frac{1}{\pi }\left[ {\left. {\left( { - \frac{{\sin nx}}{n}} \right)} \right|_{ - \pi }^{ - \large\frac{\pi }{2}\normalsize} + \left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_{\large\frac{\pi }{2}\normalsize}^\pi } \right] } = {\frac{1}{{\pi n}}\left[ { - \sin \left( { - \frac{{n\pi }}{2}} \right) + \sin \left( { - n\pi } \right) + \sin n\pi - \sin \frac{{n\pi }}{2}} \right] } = {\frac{1}{{\pi n}}\left[ {\cancel{\sin \frac{{n\pi }}{2}} - \cancel{\sin n\pi} + \cancel{\sin n\pi} - \cancel{\sin \frac{{n\pi }}{2}}} \right] = 0.} \] (Этот результат очевиден, поскольку заданная функция − нечетная.)

Определим коэффициенты разложения \({b_n}:\) \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nxdx} } = {\frac{1}{\pi }\left[ {\int\limits_{ - \pi }^{ - \large\frac{\pi }{2}\normalsize} {\left( { - \sin nx} \right)dx} + \int\limits_{\large\frac{\pi }{2}\normalsize}^\pi {\sin nxdx} } \right] } = {\frac{1}{\pi }\left[ {\left. {\left( {\frac{{\cos nx}}{n}} \right)} \right|_{ - \pi }^{ - \large\frac{\pi }{2}\normalsize} - \left. {\left( {\frac{{\cos nx}}{n}} \right)} \right|_{\large\frac{\pi }{2}\normalsize}^\pi } \right] } = {\frac{1}{{\pi n}}\left[ {\cos\left( { - \frac{{n\pi }}{2}} \right) - \cos \left( { - n\pi } \right) - \cos n\pi + \cos \frac{{n\pi }}{2}} \right] } = {\frac{1}{{\pi n}}\left[ {\cos\frac{{n\pi }}{2} - \cos n\pi - \cos n\pi + \cos \frac{{n\pi }}{2}} \right] } = {\frac{2}{{\pi n}}\left( {\cos\frac{{n\pi }}{2} - \cos n\pi } \right).} \] Таким образом, разложение в ряд Фурье определяется формулой \[f\left( x \right) = \frac{2}{\pi }\sum\limits_{n = 1}^\infty {\frac{1}{n}\left( {\cos\frac{{n\pi }}{2} - \cos n\pi } \right)\sin nx} .\] На рисунке \(6\) представлен график исходной прямоугольной функции и ее Фурье аппроксимации при \(n = 10.\)