Неравенство, в котором неизвестная переменная находится под знаком тригонометрической функции, называется тригонометрическим неравенством.

К простейшим тригонометрически неравенствам относятся следующие 16 неравенств:
sin x > a,     sin x ≥ a,     sin x < a,     sin x ≤ a,
cos x > a,     cos x ≥ a,     cos x < a,     cos x ≤ a,
tan x > a,     tan x ≥ a,     tan x < a,     tan x ≤ a,
cot x > a,     cot x ≥ a,     cot x < a,     cot x ≤ a.
Здесь x является неизвестной переменной, a может быть любым действительным числом.

При a ≥ 1 неравенство sin x > a не имеет решений:
x ∈ ∅

При a < −1 решением неравенства sin x > a является любое действительное число:
x ∈ ℜ

При −1 ≤ a < 1 решение неравенства sin x > a выражается в виде
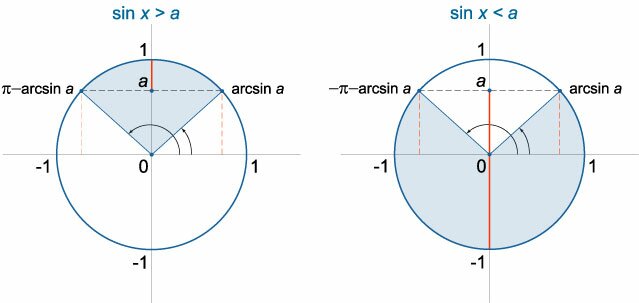
arcsin a + 2πn < x < π − arcsin a + 2πn,  n ∈ Z  (рис.1).

При a > 1 неравенство sin x ≥ a не имеет решений:
x ∈ ∅

При a ≤ −1 решением неравенства sin x ≥ a является любое действительное число:
x ∈ ℜ

Случай a = 1
x = π/2 + 2πn,  n ∈ Z

При −1 < a < 1 решение нестрогого неравенства sin x ≥ a включает граничные углы и имеет вид
arcsin a + 2πn ≤ x ≤ π − arcsin a + 2πn,  n ∈ Z  (рис.1).

При a > 1 решением неравенства sin x < a является любое действительное число:
x ∈ ℜ

При a ≤ −1 у неравенства sin x < a решений нет:
x ∈ ∅

При −1 < a ≤ 1 решение неравенства sin x < a лежит в интервале
− π − arcsin a + 2πn < x < arcsin a + 2πn,  n ∈ Z   (рис.2).

При a ≥ 1 решением неравенства sin x ≤ a является любое действительное число:
x ∈ ℜ

При a < −1 неравенства sin x ≤ a решений не имеет:
x ∈ ∅

Случай a = −1
x = − π/2 + 2πn,  n ∈ Z

При −1 < a < 1 решение нестрогого неравенства sin x ≤ a находится в интервале
− π − arcsin a + 2πn ≤ x ≤ arcsin a + 2πn,  n ∈ Z   (рис.2).

При a ≥ 1 неравенство cos x > a не имеет решений:
x ∈ ∅

При a < −1 решением неравенства cos x > a является любое действительное число:
x ∈ ℜ

При −1 ≤ a < 1 решение неравенства cos x > a имеет вид
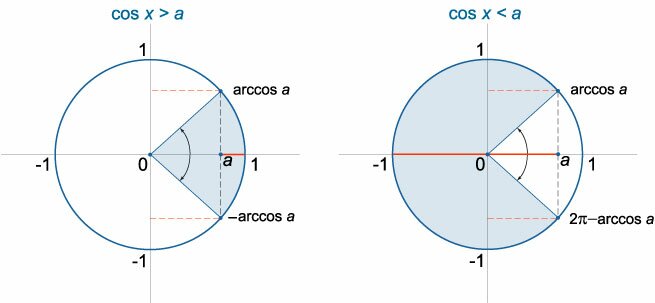
− arccos a + 2πn < x < arccos a + 2πn,  n ∈ Z  (рис.3).

При a > 1 неравенство cos x ≥ a не имеет решений:
x ∈ ∅

При a ≤ −1 решением неравенства cos x ≥ a является любое действительное число:
x ∈ ℜ

Случай a = 1
x = 2πn,  n ∈ Z

При −1 < a < 1 решение нестрогого неравенства cos x ≥ a выражается формулой
− arccos a + 2πn ≤ x ≤ arccos a + 2πn,  n ∈ Z  (рис.3).

При a > 1 неравенство cos x < a справедливо при любом действительном значении x:
x ∈ ℜ

При a ≤ −1 неравенство cos x < a не имеет решений:
x ∈ ∅

При −1 < a ≤ 1 решение неравенства cos x < a записывается в виде
arccos a + 2πn < x < 2π − arccos a + 2πn,  n ∈ Z  (рис.4).

При a ≥ 1 решением неравенства cos x ≤ a является любое действительное число:
x ∈ ℜ

При a < −1 неравенство cos x ≤ a не имеет решений:
x ∈ ∅

Случай a = −1
x = π + 2πn,  n ∈ Z

При −1 < a < 1 решение нестрогого неравенства cos x ≤ a записывается как
arccos a + 2πn ≤ x ≤ 2π − arccos a + 2πn,  n ∈ Z  (рис.4).

При любом действительном значении a решение строгого неравенства tan x > a имеет вид
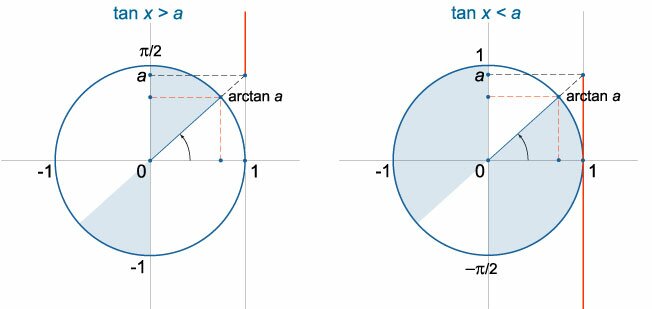
arctan a + πn < x < π/2 + πn,  n ∈ Z  (рис.5).

Для любого значения a решение неравенства tan x ≥ a выражается в виде
arctan a + πn ≤ x < π/2 + πn,  n ∈ Z  (рис.5).

Для любого значения a решение неравенства tan x < a записывается в виде
− π/2 + πn < x < arctan a + πn,  n ∈ Z  (рис.6).

При любом a неравенство tan x ≤ a имеет следующее решение:
− π/2 + πn < x ≤ arctan a + πn,  n ∈ Z  (рис.6).

При любом a решение неравенства cot x > a имеет вид
πn < x < arccot a + πn,  n ∈ Z  (рис.7).

Нестрогое неравенство cot x ≥a имеет аналогичное решение
πn < x ≤ arccot a + πn,  n ∈ Z  (рис.7).

Для любого значения a решение неравенства cot x < a лежит в открытом интервале
arccot a + πn < x < π + πn,  n ∈ Z  (рис.8).

При любом a решение нестрогого неравенства cot x ≤ a находится в полуоткрытом интервале
arccot a + πn ≤ x < π + πn,  n ∈ Z  (рис.8).