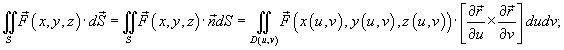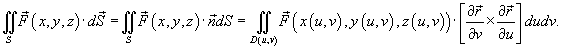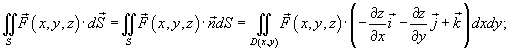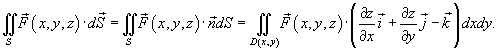|
Поверхностные интегралы второго рода
|
||||||
|
Рассмотрим векторное поле
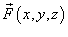 и поверхность S, которая описывается вектором и поверхность S, которая описывается вектором
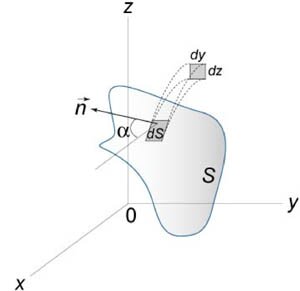
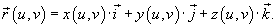 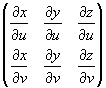 Обозначим через 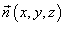 единичный нормальный вектор к поверхности S в точке единичный нормальный вектор к поверхности S в точке 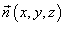 непрерывна, то в каждой точке поверхности существуют два противоположно направленных единичных нормальных вектора: непрерывна, то в каждой точке поверхности существуют два противоположно направленных единичных нормальных вектора:
 Если S является границей ограниченной области, то ее можно ориентировать внешней или внутренней нормалями. Поверхность S, ориентированную внешней нормалью, называют ее внешней стороной, а ориентированную внутренней нормалью, − ее внутренней стороной. Поверхностный интеграл второго рода от векторного поля 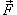 по ориентированной поверхности S (или поток векторного поля по ориентированной поверхности S (или поток векторного поля 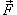 через поверхность S) может быть записан в одной из следующих форм: через поверхность S) может быть записан в одной из следующих форм:
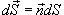 называется векторным элементом поверхности. Точка обозначает скалярное произведение соответствующих векторов. Частные производные, входящие в последние формулы, вычисляются следующим образом: называется векторным элементом поверхности. Точка обозначает скалярное произведение соответствующих векторов. Частные производные, входящие в последние формулы, вычисляются следующим образом:
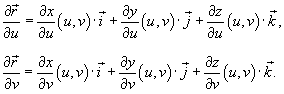 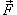 по поверхности S записывается в одной из следующих форм: по поверхности S записывается в одной из следующих форм:
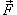 . Введем . Введем 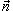 к поверхности S. Тогда скалярное произведение к поверхности S. Тогда скалярное произведение 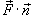 равно равно
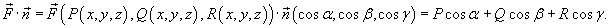 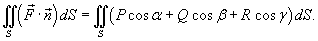 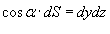 (рисунок 1), и, аналогично, (рисунок 1), и, аналогично, 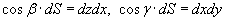 , получаем следующую формулу для вычисления поверхностного интеграла II рода: , получаем следующую формулу для вычисления поверхностного интеграла II рода:
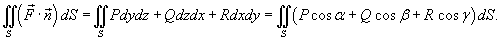 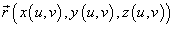 , то последняя формула принимает вид , то последняя формула принимает вид
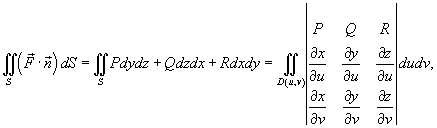
|
||||||
|
Пример 1
|
||||||
|
Вычислить поверхностный интеграл от векторного поля
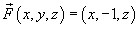 по внутренне ориентированной поверхности S, заданной уравнением по внутренне ориентированной поверхности S, заданной уравнением 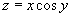 , где , где 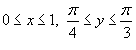 . .
Решение. 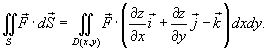 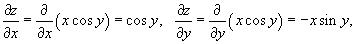 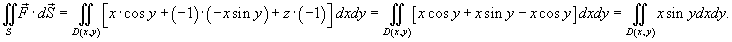 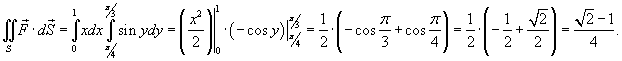 |
||||||
|
Пример 2
|
||||||
|
Найти интеграл от векторного поля
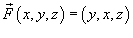 по поверхности S, заданной в параметрической форме вектором по поверхности S, заданной в параметрической форме вектором 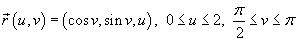 . .
Решение. 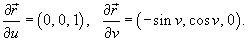 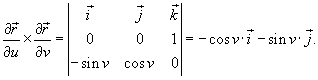 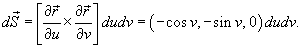 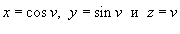 , то векторное поле , то векторное поле 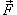 можно представить в виде: можно представить в виде:
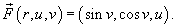  |
||||||
|
Пример 3
|
||||||
|
Оценить поток векторного поля
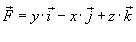 через коническую поверхность через коническую поверхность 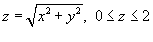 , ориентированную внешней стороной. , ориентированную внешней стороной.
Решение. 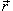 : :
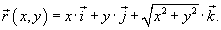 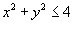 . .Найдем векторный элемент площади 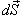 , перпендикулярный поверхности и направленный во внешнюю сторону. Определим частные производные: , перпендикулярный поверхности и направленный во внешнюю сторону. Определим частные производные:
 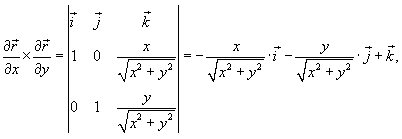 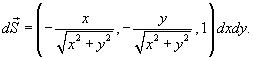 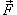 на поверхности конуса можно записать в виде на поверхности конуса можно записать в виде
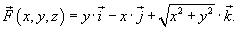 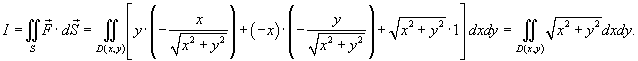 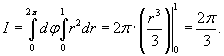 |
||||||
|
Пример 4
|
||||||
|
Оценить поток векторного поля
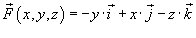 через внутреннюю сторону единичной сферы через внутреннюю сторону единичной сферы 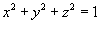 . .
Решение. 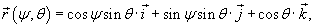 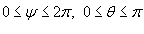 . В результате вектор . В результате вектор 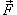 на заданной поверхности можно записать в виде на заданной поверхности можно записать в виде
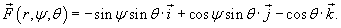 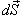 . Частные производные равны . Частные производные равны
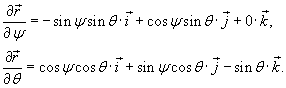 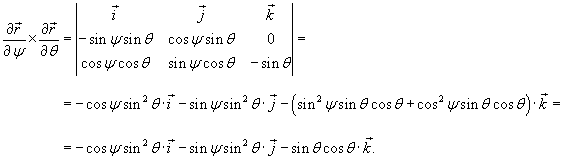 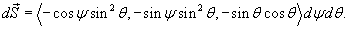  |
||||||
|
Пример 5
|
||||||
|
Вычислить интеграл
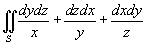 , где S − часть внутренней поверхности эллипсоида, заданного параметрически в виде , где S − часть внутренней поверхности эллипсоида, заданного параметрически в виде 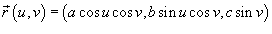 . Параметры u,v изменяются в интервале . Параметры u,v изменяются в интервале 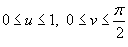 . .
Решение.  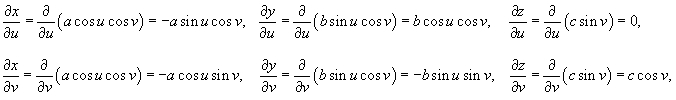 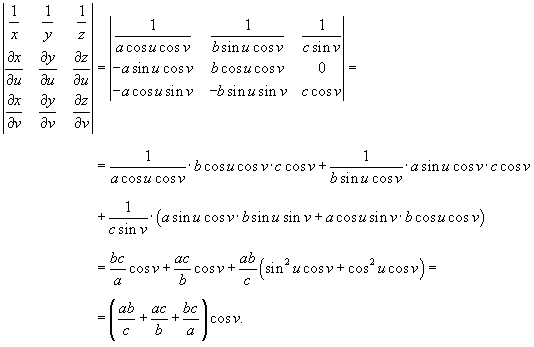 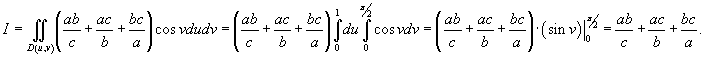 |
||||||
|
Пример 6
|
||||||
|
Найти интеграл
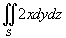 , где S − внутренняя поверхность сферы , где S − внутренняя поверхность сферы 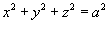 . .
Решение. 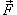 : :
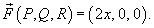 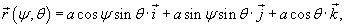 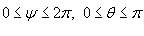 . Применим формулу . Применим формулу
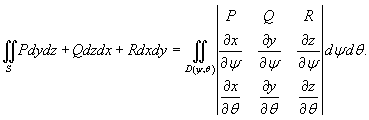 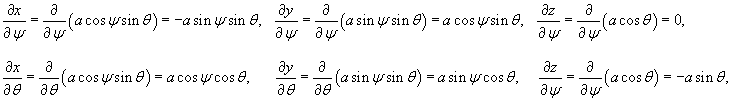 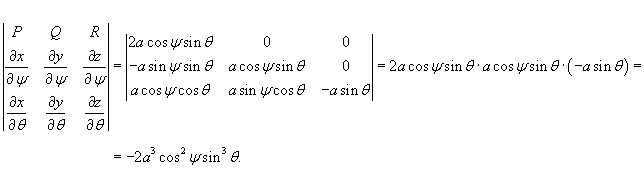 Искомый поверхностный интеграл будет равен 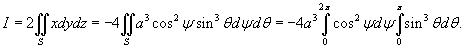 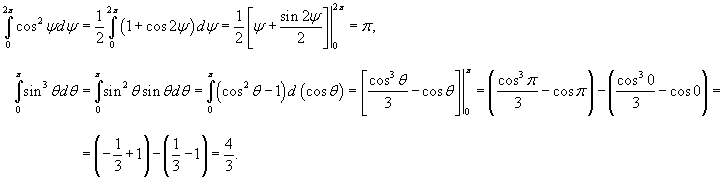 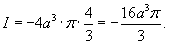 |
||||||