|
Поверхностные интегралы первого рода
|
||||||
|
Рассмотрим скалярную функцию
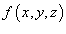 и поверхность S. Пусть S задана векторной функцией и поверхность S. Пусть S задана векторной функцией
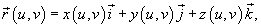 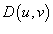 в плоскости uv. Заметим, что функция в плоскости uv. Заметим, что функция 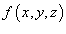 рассматривается только в точках, принадлежащих поверхности S, то есть рассматривается только в точках, принадлежащих поверхности S, то есть
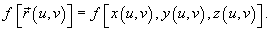 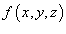 по поверхности S определяется следующим образом: по поверхности S определяется следующим образом:
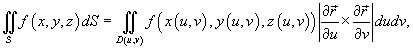 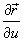 и и 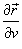 равны равны
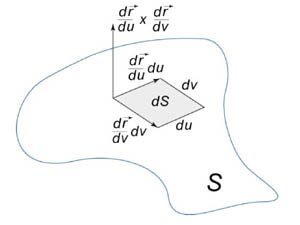
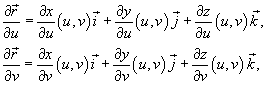 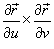 означает векторное произведение. Вектор означает векторное произведение. Вектор 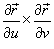 перпендикулярен поверхности в точке перпендикулярен поверхности в точке 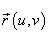 . .Абсолютное значение 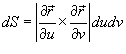 называется элементом площади: оно соответствует изменению площади dS в результате приращения координат u и v на малые значения du и dv (рисунок 1). называется элементом площади: оно соответствует изменению площади dS в результате приращения координат u и v на малые значения du и dv (рисунок 1).
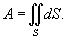 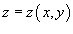 , где , где  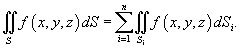 |
||||||
|
Пример 1
|
||||||
|
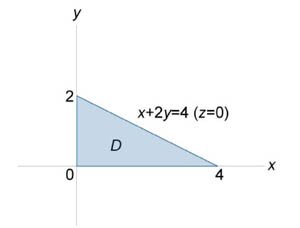
Вычислить поверхностный интеграл
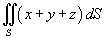 , где S − часть плоскости , где S − часть плоскости 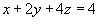 , лежащая в первом октанте , лежащая в первом октанте Решение. 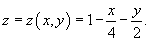 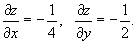 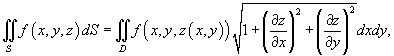 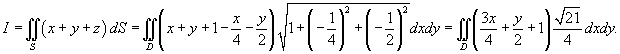 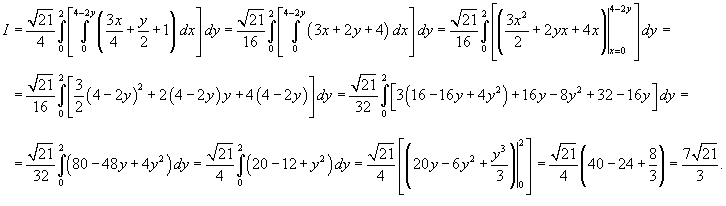 |
||||||
|
Пример 2
|
||||||
|
Вычислить интеграл
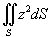 , где S представляет собой полную поверхность конуса , где S представляет собой полную поверхность конуса 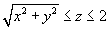 . .
Решение. 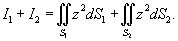 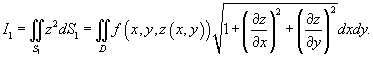 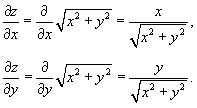 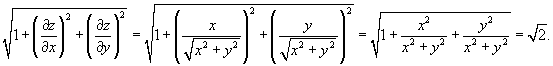 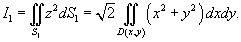 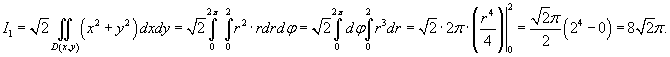 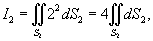 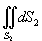 равно площади основания равно площади основания 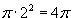 . Тогда . Тогда
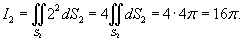 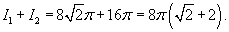
|
||||||
|
Пример 3
|
||||||
|
Вычислить интеграл
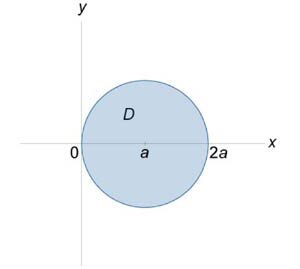
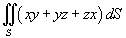 , где S − часть конуса , где S − часть конуса 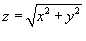 внутри поверхности внутри поверхности 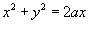 . .
Решение. 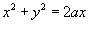 в следующем виде: в следующем виде:
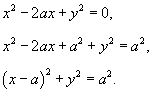  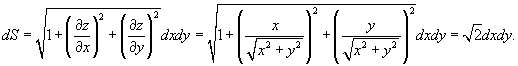 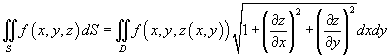 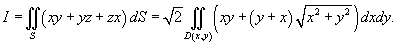 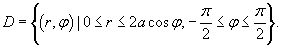 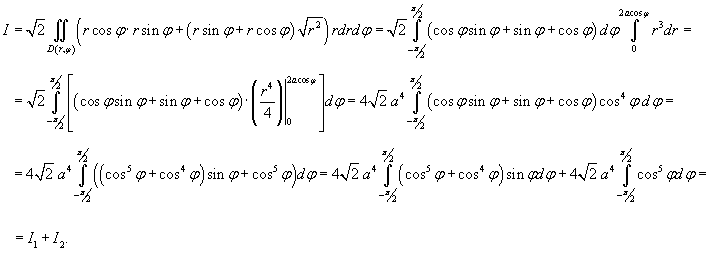 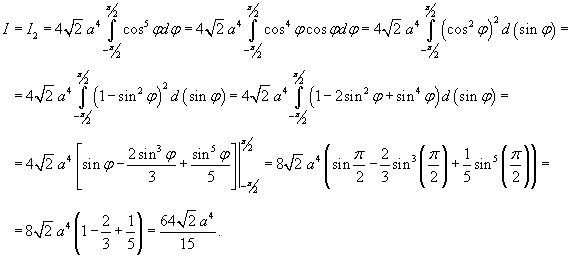 |
||||||
|
Пример 4
|
||||||
|
Найти интеграл
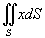 , где поверхность S − часть сферы , где поверхность S − часть сферы 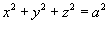 , лежащая в первом октанте. , лежащая в первом октанте.
Решение. 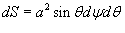 . Поскольку . Поскольку 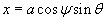 , то интеграл можно записать в следующей форме: , то интеграл можно записать в следующей форме:
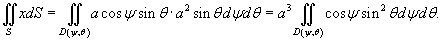 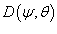 определяется как определяется как
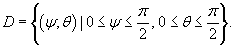 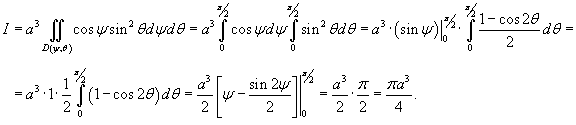 |
||||||
|
Пример 5
|
||||||
|
Найти интеграл
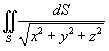 , где S − часть цилиндрической поверхности, заданной параметрически в виде , где S − часть цилиндрической поверхности, заданной параметрически в виде 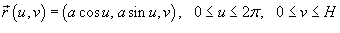 . .
Решение. 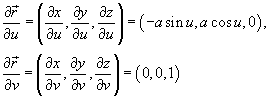 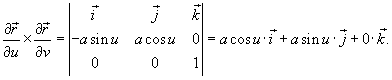 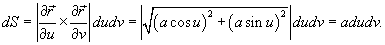 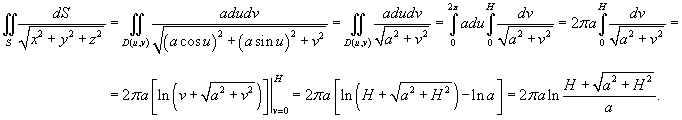 |
||||||
|
Пример 6
|
||||||
|
Вычислить интеграл
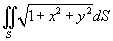 . Поверхность S задана параметрически в виде . Поверхность S задана параметрически в виде 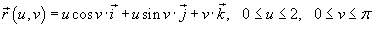 . .
Решение. 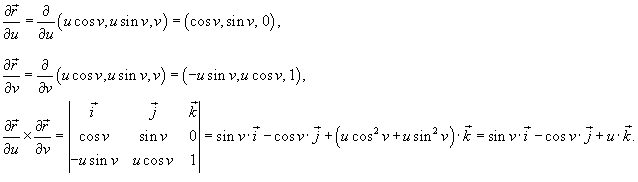 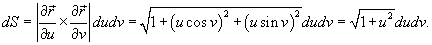 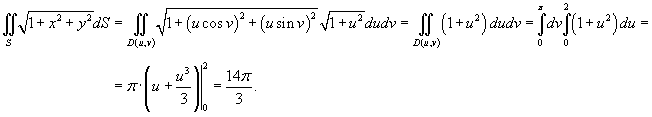 |
||||||