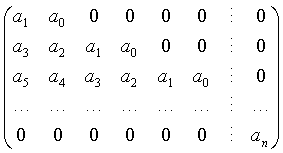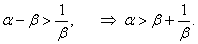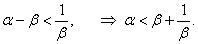|
Критерий Рауса-Гурвица
|
||||||
|
Рассмотрим однородную систему дифференциальных уравнений n-го порядка с постоянными коэффициентами:
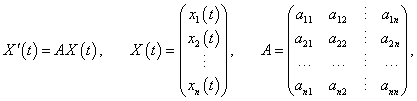 Нелинейную автономную систему можно также свести к такой системе, выполнив линеаризацию вблизи точки равновесия. Далее без потери общности будем считать, что точка равновесия находится в начале координат. Этого всегда можно достигнуть выбором подходящей системы координат. Устойчивость или неустойчивость положения равновесия определяется знаками действительных частей собственных значений матрицы A. Чтобы найти собственные значения λ, необходимо решить характеристическое уравнение 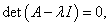 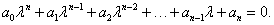 В такой ситуации большое значение имеют методы, позволяющие, не решая само характеристическое уравнение, определить, будут ли все его корни иметь отрицательную действительную часть, т.е. установить устойчивость системы. Одним из таких методов является критерий Рауса-Гурвица, который содержит необходимые и достаточные условия устойчивости системы. Рассмотрим снова характеристическое уравнение 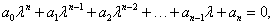
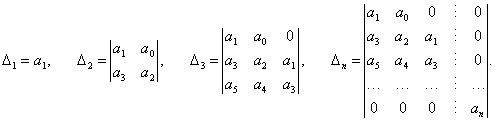 Для наиболее распространенных систем 2-го, 3-го и 4-го порядков получаем следующие критерии устойчивости: Для системы 2-го порядка условие устойчивости выглядит так: 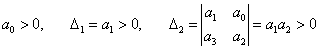 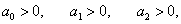 Для системы 3-го порядка критерий устойчивости определяется неравенствами 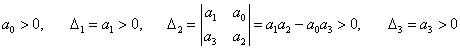 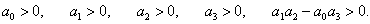 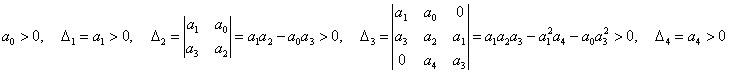 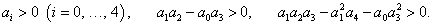
|
||||||
|
Пример 1
|
||||||
|
Исследовать устойчивость нулевого решения уравнения
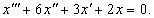
Решение.
Запишем характеристическое уравнение:
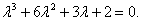 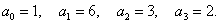 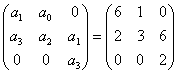 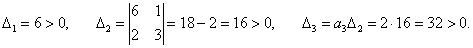 |
||||||
|
Пример 2
|
||||||
|
Исследовать на устойчивость нулевое решение дифференциального уравнения
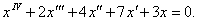
Решение.
Составим характеристическое уравнение:
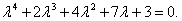 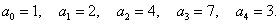 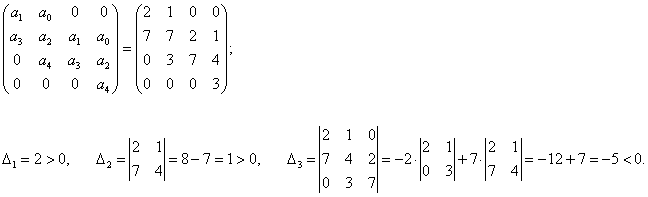 |
||||||
|
Пример 3
|
||||||
|
При каких значениях параметров α и β нулевое решение уравнения
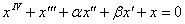
Решение.
Характеристическое уравнение записывается в виде
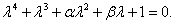 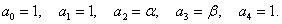 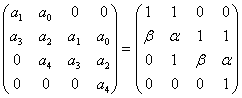 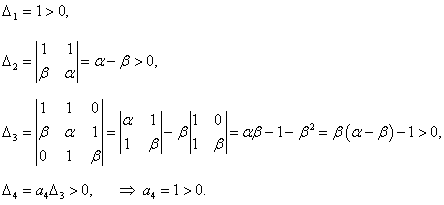 
Итак, решением неравенства являются две бесконечные области, симметричные относительно начала координат и ограниченные кривой
|
||||||
|
Пример 4
|
||||||
|
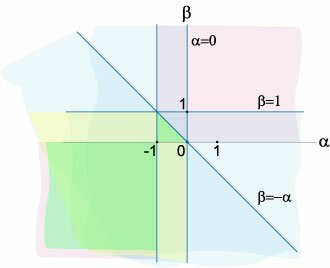
Исследовать, при каких значениях параметров α и β нулевое решение системы является асимптотически устойчивым:
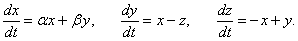
Решение.
Составим характеристическое уравнение:
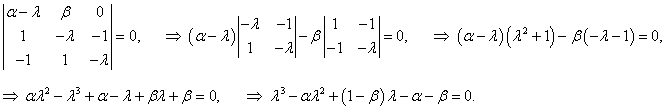 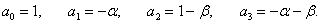 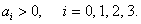 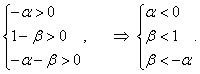 Теперь рассмотрим достаточные условия устойчивости. Запишем матрицу Гурвица: 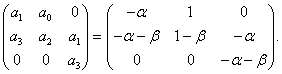 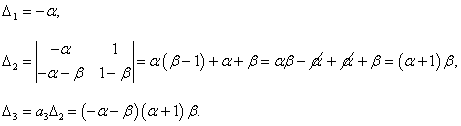 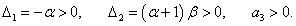 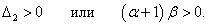
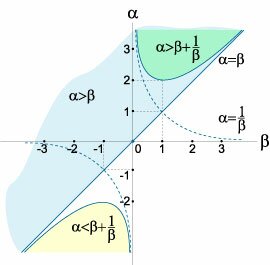
Область устойчивости системы ограничена значениями параметров α, β, при которых выполняются как необходимые, так и достаточные условия асимптотической устойчивости. Эта область состоит из левого нижнего квадранта, ограниченного прямыми |
||||||