|
Признак Даламбера. Радикальный признак Коши
|
|
Признак Даламбера
Пусть  − ряд с положительными членами. Тогда справедливы следующие свойства: − ряд с положительными членами. Тогда справедливы следующие свойства:
Радикальный признак Коши
Снова рассмотрим ряд  с положительными членами. Согласно признаку Коши: с положительными членами. Согласно признаку Коши:
|
|
Пример 1
|
|
Исследовать на сходимость ряд
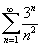 . .
Решение.
Воспользуемся признаком Даламбера.
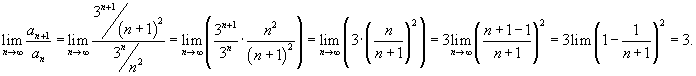 |
|
Пример 2
|
|
Исследовать на сходимость ряд
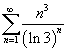 . .
Решение.
Применим признак Даламбера.
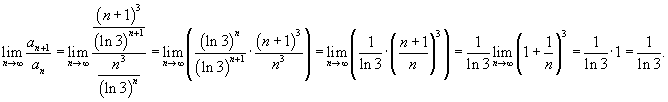 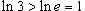 и и 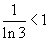 , то заданный ряд сходится. , то заданный ряд сходится. |
|
Пример 3
|
|
Определить, сходится или расходится ряд
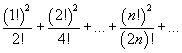
Решение.
В соответствии с признаком Даламбера, вычислим следующий предел:
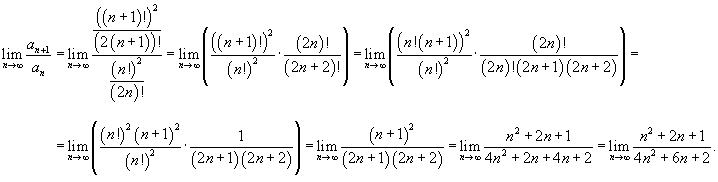 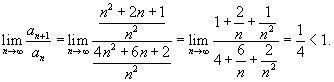 |
|
Пример 4
|
|
Исследовать на сходимость ряд
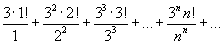
Решение.
Применим признак Даламбера и вычислим соответствующий предел:
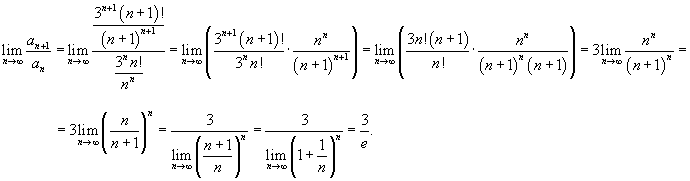 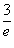 больше 1, то данный ряд будет расходиться. больше 1, то данный ряд будет расходиться. |
|
Пример 5
|
|
Определить, сходится или расходится ряд
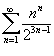 . .
Решение.
Используем радикальный признак Коши.
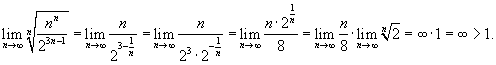 |
|
Пример 6
|
|
Исследовать на сходимость ряд
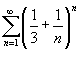 . .
Решение.
Применяя признак Коши, вычислим следующий предел:
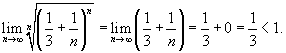 |
|
Пример 7
|
|
Исследовать на сходимость следующий ряд:
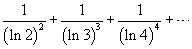
Решение.
Общий член ряда выражается формулой 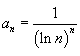 . Применим радиальный признак Коши: . Применим радиальный признак Коши:
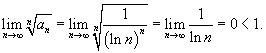 |
 , то ряд
, то ряд  , то ряд
, то ряд  , то ряд
, то ряд  , то ряд
, то ряд  , то ряд
, то ряд  , то вопрос о сходимости ряда
, то вопрос о сходимости ряда