|
Радиоактивный распад
|
||||||
|
В природе существует большое число атомных ядер, которые могут спонтанно излучать элементарные частицы или ядерные фрагменты. Такое явление называется радиоактивным распадом. Этот эффект изучали на рубеже 19-20 веков Антуан Беккерель, Мария и Пьер Кюри, Фредерик Содди, Эрнест Резерфорд и другие ученые. В результате экспериментов, Ф.Содди и Э.Резерфорд вывели закон радиоактивного распада, который описывается дифференциальным уравнением
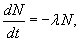 Данное уравнение легко решить, и решение имеет вид: 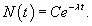 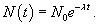
Периодом полураспада T радиоактивного материала называется время, необходимое для распада половины первоначального количества вещества. Следовательно, в момент T: 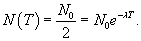 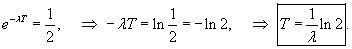 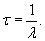 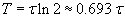 |
||||||
|
Пример 1
|
||||||
|
Найти массу радиоактивного материала через промежуток времени, равный трем периодам полураспада. Начальная масса составляла 80г.
Решение. 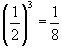 от первоначального количества. Следовательно, через заданный промежуток времени масса вещества будет равна от первоначального количества. Следовательно, через заданный промежуток времени масса вещества будет равна 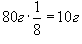 . . |
||||||
|
Пример 2
|
||||||
|
Начальная масса изотопа йода составляла 200г. Определить массу йода спустя 30 дней, если период полураспада данного изотопа 8 дней.
Решение. 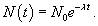  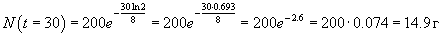 |
||||||
|
Пример 3
|
||||||
|
Радиоактивный изотоп индий-111 часто используется в радиоизотопной медицинской диагностике и лучевой терапии. Его период полураспада составляет 2,8 дней. Какова была первоначальная масса изотопного вещества, если через две недели осталось 5г?
Решение. 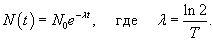 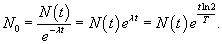  |
||||||
|
Пример 4
|
||||||
|
Найти период полураспада радиоактивного вешщества, если активность каждый месяц уменьшается на 10%.
Решение. 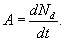 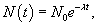 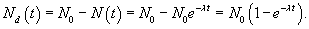 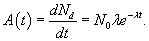 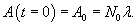 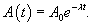 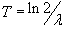 в последнюю формулу, получаем: в последнюю формулу, получаем:
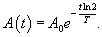 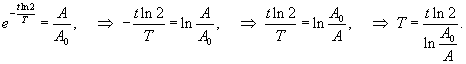 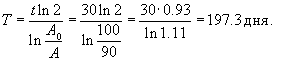 |
||||||

