|
|
|
|
Свойства степенных рядов
|
|
Функциональный ряд: 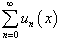
Функции: f( x), u0( x), u1( x), ..., un( x)
Степенные ряды: 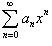 , 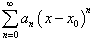
|
Коэффициенты степенного ряда: a0, a1, ..., an
Радиус сходимости: R
Действительные числа: x, x0
Целые числа: n
|
-
Ряд, члены которого являются функциями, называется функциональным рядом. В общем виде функциональный ряд записывается как
где ui (x) − функции переменной x.
-
Функциональный ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:
где ai − коэффициенты степенного ряда (постоянные действительные числа).
-
Часто рассматривается степенной ряд, расположенный по степеням (x − x0):
где точка x0 называется центром степенного ряда.
-
Интервал сходимости степенного ряда
Рассмотрим функцию 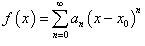 . Ее областью определения является множество значений x, при которых ряд сходится. Данная область определения называется интервалом сходимости. . Ее областью определения является множество значений x, при которых ряд сходится. Данная область определения называется интервалом сходимости.
-
Радиус сходимости степенного ряда
Если интервал сходимости представляется в виде (x0 − R, x0 + R), где R > 0, то величина R называется радиусом сходимости. Степенной ряд сходится абсолютно в каждой точке интервала сходимости. Сходимость в граничных точках x0 − R и x0 + R устанавливается отдельно.
-
Радиус сходимости по признаку Даламбера
-
Радиус сходимости по радикальному признаку Коши
-
Дифференцирование степенных рядов
Пусть дан степенной ряд
имеющий радиус сходимости R > 0. Функция 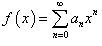 является непрерывной при |x| < R. Степенной ряд внутри интервала сходимости можно дифференцировать почленно. Производная степенного ряда равна является непрерывной при |x| < R. Степенной ряд внутри интервала сходимости можно дифференцировать почленно. Производная степенного ряда равна
-
Интегрирование степенных рядов
Степенной ряд можно почленно интегрировать на отрезке, расположенном внутри интервала сходимости. Если −R < b < x < R, то справедливо соотношение
Если интегрирование выполняется на отрезке [0, x], то интеграл выражается формулой
|
|
|
|