|
Свойства пределов
|
|
Обозначение предела
Предел функции обозначается как 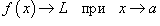 или через символ предела: или через символ предела: 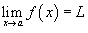 . .Всюду ниже предполагается, что пределы функций 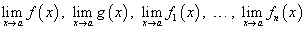 существуют. существуют.
Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
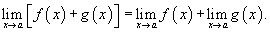
Расширенное правило суммы
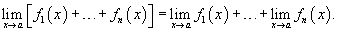
Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
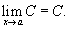
Предел произведения функции на постоянную величину
Постоянный коэффициент можно выносить за знак предела:
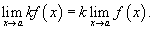
Предел произведения
Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
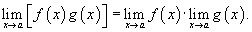
Расширенное правило произведения
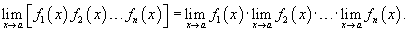
Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
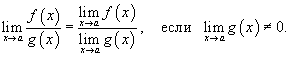
Предел степенной функции
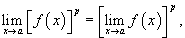 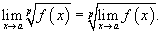 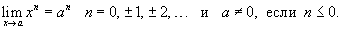
Предел показательной функции
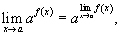
Предел логарифмической функции
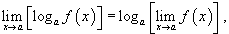
Теорема "о двух милиционерах"
Предположим, что 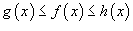 для всех x близких к a, за исключением, быть может, самой точки для всех x близких к a, за исключением, быть может, самой точки 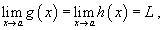 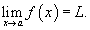 |
|
Пример 1
|
|
Найти предел
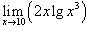 . .
Решение. 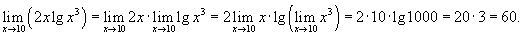 |
|
Пример 2
|
|
Найти предел
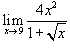 . .
Решение. 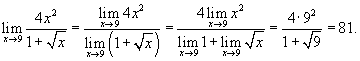 |
|
Пример 3
|
|
Зная, что
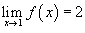 и и 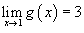 , вычислить предел , вычислить предел 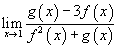 . .
Решение. 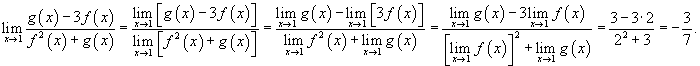 |
|
Пример 4
|
|
Вычислить предел
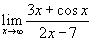 . .
Решение. 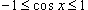 для всех x. Тогда можно записать для всех x. Тогда можно записать
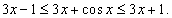 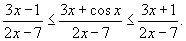 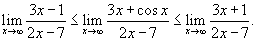 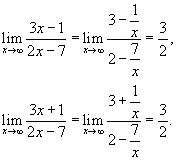 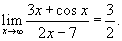 |
|
Пример 5
|
|
Вычислить предел
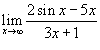 . .
Решение. 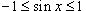 для всех x. Тогда для всех x. Тогда
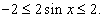 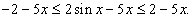 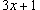 , получаем , получаем
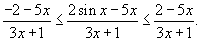 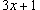 является положительным числом при является положительным числом при 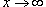 .) .)Вычислим левый и правый пределы. 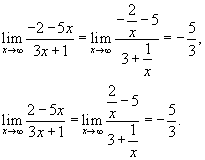 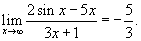 |