|
|
|
|
Свойства бесконечных рядов
|
|
|
Числовые последовательности: {an}, {bn}
Первые члены ряда: a1, b1
N-ые члены ряда: an, bn
Частичная сумма ряда: Sn
Число членов ряда: n
|
Сумма бесконечного ряда: L, A, B
Действительное число: c
Непрерывная функция: f(x)
Независимая переменная: x
|
-
Определение бесконечного числового ряда
Пусть задана числовая последовательность {an}. Бесконечным рядом называется сумма вида
-
Частичная сумма ряда
-
Сходимость бесконечного числового ряда
Ряд сходится к L, если его частичные суммы {Sn} сходятся к L при n → ∞:
-
Необходимый признак сходимости числового ряда
Если ряд 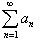 сходится, то сходится, то 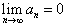 . .
Обратное утверждение неверно.
-
Достаточное условие расходимости ряда
Если 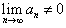 или данный предел не существует, то числовой ряд или данный предел не существует, то числовой ряд 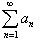 расходится. расходится.
-
Линейные свойства сходящихся рядов
Пусть даны два сходящихся ряда 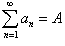 и и 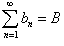 . Тогда справедливы следующие свойства: . Тогда справедливы следующие свойства:
где c − действительное число.
-
Признаки сравнения рядов
Пусть даны два ряда 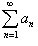 и и 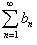 − такие, что для всех n выполняется условие 0 < an ≤ bn. Тогда справедливы следующие признаки сравнения: − такие, что для всех n выполняется условие 0 < an ≤ bn. Тогда справедливы следующие признаки сравнения:
• Если 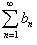 сходится, то сходится, то 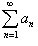 также сходится; также сходится;
• Если 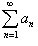 расходится, то расходится, то 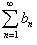 также расходится. также расходится.
-
Предельные признаки сравнения рядов
Даны два ряда 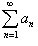 и и 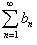 , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки: , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки:
• Если 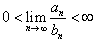 , то оба ряда , то оба ряда 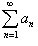 и и 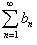 либо сходятся, либо расходятся; либо сходятся, либо расходятся;
• Если 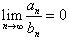 , то ряд , то ряд 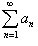 сходится, если сходится ряд сходится, если сходится ряд 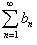 ; ;
• Если 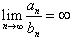 , то ряд , то ряд 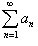 расходится, если расходится ряд расходится, если расходится ряд 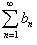 . .
-
Обобщенный гармонический ряд
Обобщенный гармонический ряд 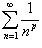 сходится при p > 1 и расходится при 0 < p ≤ 1. сходится при p > 1 и расходится при 0 < p ≤ 1.
-
Интегральный признак Коши
Предположим, что f(x) является непрерывной, положительной и убывающей функцией для всех x ≥ 1. Тогда ряд
сходится, если сходится несобственный интеграл 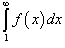 , и расходится, если , и расходится, если 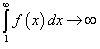 . .
-
Признак Даламбера
Пусть 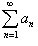 − числовой ряд с положительными членами. Тогда справедливы следующие свойства: − числовой ряд с положительными членами. Тогда справедливы следующие свойства:
• Если 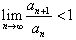 , то ряд , то ряд 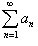 сходится; сходится;
• Если 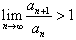 , то ряд , то ряд 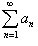 расходится; расходится;
• Если 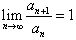 , то ряд , то ряд 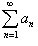 может как сходиться, так и расходиться. В этом случае для исследования сходимости ряда нужно использовать другие признаки. может как сходиться, так и расходиться. В этом случае для исследования сходимости ряда нужно использовать другие признаки.
-
Радикальный признак Коши
Рассмотрим ряд 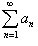 с положительными членами. В соответствии с признаком Коши: с положительными членами. В соответствии с признаком Коши:
• Если  , то ряд , то ряд 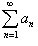 сходится; сходится;
• Если 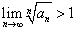 , то ряд , то ряд 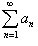 расходится; расходится;
• Если 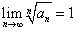 , то здесь также, как и в случае признака Даламбера, вопрос о сходимости ряда остается открытым. , то здесь также, как и в случае признака Даламбера, вопрос о сходимости ряда остается открытым.
|
|
|
|