Пусть действительная функция f(x) определена и ограничена на отрезке [a, b]. Разобьем данный отрезок на n частичных интервалов. В каждом интервале выберем произвольную точку ξ_i и составим интегральную сумму 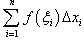, где Δx_i − длина i-го интервала. Определенным интегралом от функции f(x) на отрезке [a, b] называется предел интегральной суммы (суммы Римана) при стремлении максимальной длины частичного интервала к нулю.

Определенный интеграл от единицы равен длине интервала интегрирования:

Постоянный множитель можно выносить за знак определенного интеграла:

Определенный интеграл от суммы функций равен сумме интегралов от этих функций:

Определенный интеграл от разности функций равен разности интегралов от этих функций:

Если верхний предел равен нижнему, то определенный интеграл равен нулю:

При перестановке пределов интегрирования определенный интеграл изменяет знак на противоположный:

Пусть точка c принадлежит отрезку [a, b]. Тогда определенный интеграл от функции f(x) на отрезке [a, b] равен сумме интегралов на частичных промежутках [a, c] и [c, b]:

Определенный интеграл от неотрицательной функции всегда больше или равен нулю:

Определенный интеграл от неположительной функции всегда меньше или равен нулю:

Формула Ньютона-Лейбница

Метод подстановки для определенного интеграла

Интегрирование по частям

Приближенное вычисление определенного интеграла по формуле трапеций

Приближенное вычисление определенного интеграла по формуле Симпсона (метод парабол)

Площадь криволинейной трапеции

Площадь между двумя кривыми