|
|
|
|
Свойства знакопеременных рядов
|
|
Числовая последовательность: { an}
Знакопеременные ряды:  , 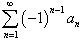
Число членов ряда: n
|
Частичная сумма ряда: Sn
Сумма ряда: S
|
-
Числовой ряд, содержащий бесконечное множество положительных членов и бесконечное множество отрицательных членов, называется знакопеременным рядом.
-
Частным случаем знакопеременного ряда является знакочередующийся ряд, в котором последовательные члены имеют противоположные знаки.
-
Признак Лейбница
Признак Лейбница является достаточным условием сходимости знакочередующегося ряда.
Пусть {an} представляет собой положительный числовой ряд, такой, что
• an+1 < an для всех n;
• 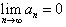 . .
Тогда знакочередующиеся ряды 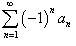 и и 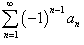 сходятся. сходятся.
-
Оценка остатка знакочередующегося ряда
Пусть знакочередующийся числовой ряд сходится по признаку Лейбница и его сумма равна S. Обозначим через Sn частичную сумму ряда, включающую n членов. Тогда остаток знакочередующегося ряда по абсолютной величине меньше модуля первого отброшенного слагаемого:
|S − Sn| < |an+1|.
-
Абсолютная сходимость ряда
Ряд  называется абсолютно сходящимся, если ряд называется абсолютно сходящимся, если ряд 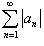 , составленный из модулей членов an, также сходится. Если ряд , составленный из модулей членов an, также сходится. Если ряд  сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение, вообще говоря, неверно. сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение, вообще говоря, неверно.
-
Условная сходимость ряда
Ряд  называется условно сходящимся, если сам он сходится, а ряд называется условно сходящимся, если сам он сходится, а ряд 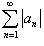 , составленный из модулей членов an, расходится. Другими словами, ряд является условно сходящимся, если он сходится, но не абсолютно. , составленный из модулей членов an, расходится. Другими словами, ряд является условно сходящимся, если он сходится, но не абсолютно.
|
|
|
|