|
Степенные ряды
|
|
Определение
Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:
 
Интервал и радиус сходимости
Рассмотрим функцию 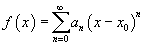 . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости. . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.Если интервал сходимости представляется в виде  , где , где Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле   |
|
Пример 1
|
|
Найти радиус и интервал сходимости степенного ряда
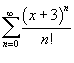 . .
Решение.
Сделаем замену: 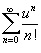 . Вычислим радиус сходимости: . Вычислим радиус сходимости:
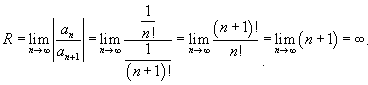 |
|
Пример 2
|
|
Определить радиус и интервал сходимости степенного ряда
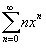 . .
Решение.
Вычислим радиус сходимости:
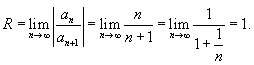 Если 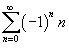 . .Если 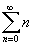 также расходится. также расходится.Следовательно, исходный ряд 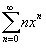 сходится на открытом интервале сходится на открытом интервале |
|
Пример 3
|
|
Найти радиус и интервал сходимости ряда
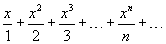
Решение.
Здесь 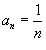 и и 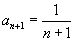 . Радиус сходимости будет равен . Радиус сходимости будет равен
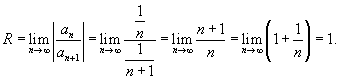 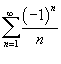 . .При 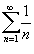 . .Таким образом, заданный ряд сходится 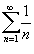 сходится на полуоткрытом интервале сходится на полуоткрытом интервале |
|
Пример 4
|
|
При каких значениях x ряд
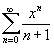 сходится? сходится?
Решение.
Найдем радиус и интервал сходимости данного ряда.
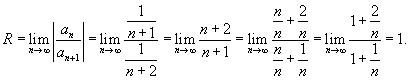 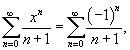 Если же 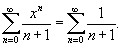 |
|
Пример 5
|
|
Найти радиус и интервал сходимости степенного ряда
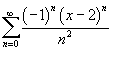 . .
Решение.
Сделаем замену: 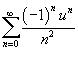 . Вычислим радиус сходимости: . Вычислим радиус сходимости:
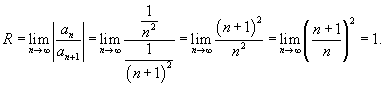 Если 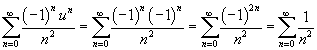 Если 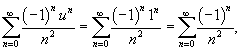 Таким образом, интервал сходимости для ряда 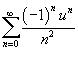 равен равен 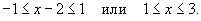 |
|
Пример 6
|
|
Найти радиус и интервал сходимости степенного ряда
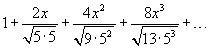
Решение.
Общий член данного степенного ряда (начиная с 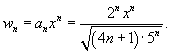 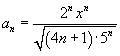 и и 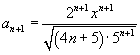 . .Определим радиус сходимости:  При 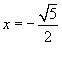 получаем получаем
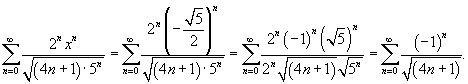 При 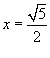 , соответственно, имеем ряд , соответственно, имеем ряд
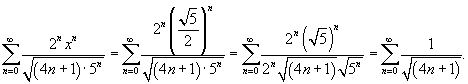 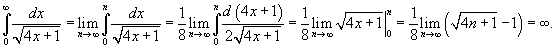 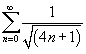 расходится. Поэтому, интервал сходимости исходного ряда равен расходится. Поэтому, интервал сходимости исходного ряда равен 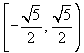 . .
|