|
Физические приложения тройных интегралов
|
||||||
|
Масса и статические моменты тела
Пусть тело занимает объем U и его объемная плотность в точке 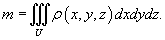 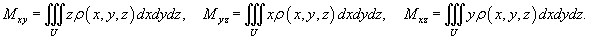 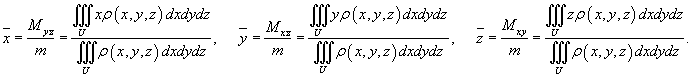
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей Oxy, Oxz, Oyz определяются выражениями
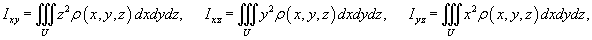 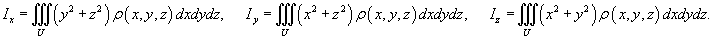 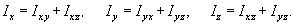 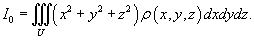 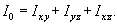
Тензор инерции
Используя рассмотренные выше 6 чисел Ix, Iy, Iz, Ixy, Ixz, Iyz, можно составить так называемую матрицу инерции или тензор инерции тела:
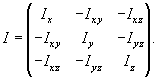 Если тело вращается вокруг оси, не совпадаюшей с главной осью инерции, то оно будет испытывать вибрации при высоких скоростях вращения. Поэтому, при конструировании таких устройств необходимо, чтобы ось вращения совпадала с одной из главных осей инерции. Например, при замене шин автомобиля проводится их балансировка: небольшие грузики добавляются к колесам, чтобы обеспечить совпадение оси вращения с главной осью инерции и исключить вибрации.
Гравитационный потенциал и сила тяготения
Ньютоновым потенциалом тела в точке 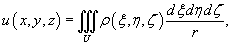 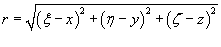 . .Интегрирование выполняется по всему объему тела. Зная потенциал, можно вычислить силу притяжения материальной точки массы m и заданного распределенного тела с плотностью 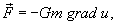 |
||||||
|
Пример 1
|
||||||
|
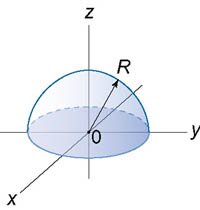
Найти центроид однородного полушара радиусом R.
Решение.
Очевидно, что в силу симметрии 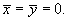 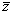 по формуле по формуле
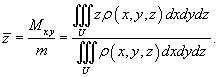 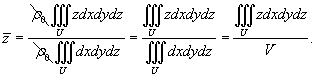  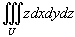 . Для этого перейдем к сферическим координатам. При этом радиальную координату будем обозначать через r − чтобы не путать с плотностью ρ. Получаем: . Для этого перейдем к сферическим координатам. При этом радиальную координату будем обозначать через r − чтобы не путать с плотностью ρ. Получаем:
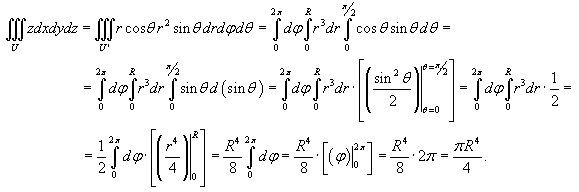 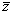 равна равна
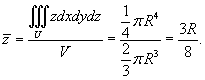 |
||||||
|
Пример 2
|
||||||
|
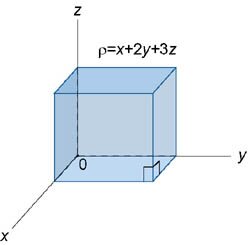
Определить массу и координаты центра тяжести единичного куба с плотностью
(рисунок 2). Решение. 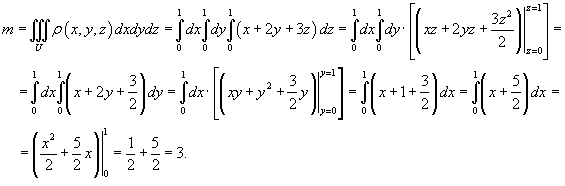 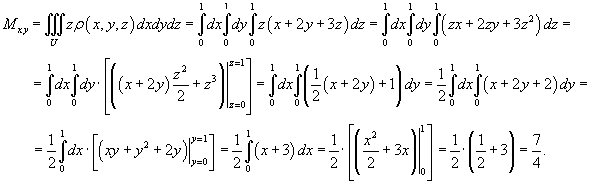 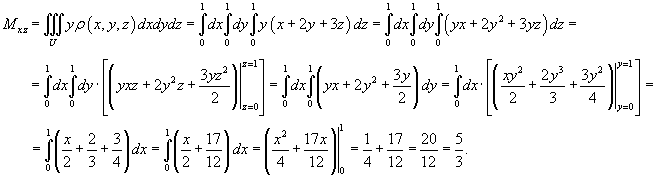 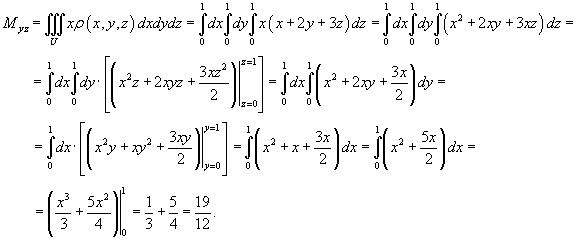 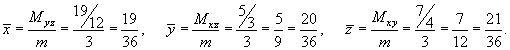 |
||||||
|
Пример 3
|
||||||
|
Найти массу шара радиуса R, плотность γ которого пропорциональна квадрату расстояния от центра.
Решение. 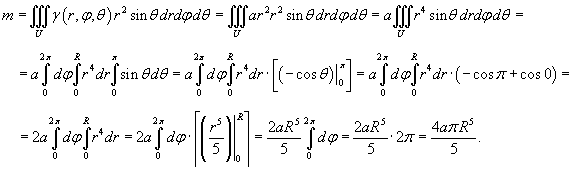 |
||||||
|
Пример 4
|
||||||
|
Найти момент инерции прямого круглого однородного конуса относительно его оси. Конус имеет радиус основания R, высоту H и общую массу m (рисунок 3).
Решение. 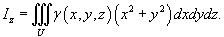 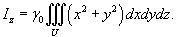 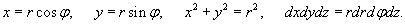 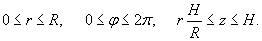 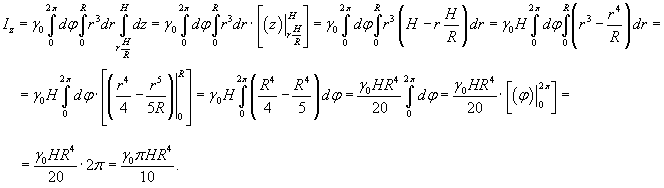 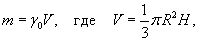 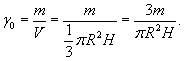 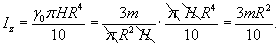 |
||||||
|
Пример 5
|
||||||
|
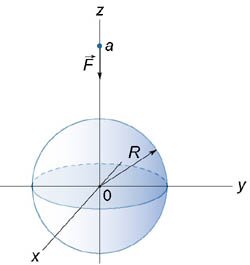
С какой силой притягивает однородный шар массы M материальную точку массы m, расположенную на расстоянии a от центра шара
Решение.
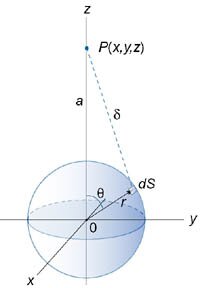
Итак, вычислим потенциал сферы произвольного радиуса r 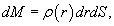 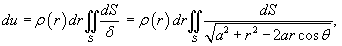 Учитывая, что элемент площади равен 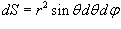 , получаем , получаем
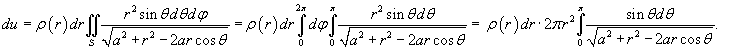 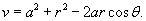 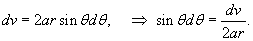 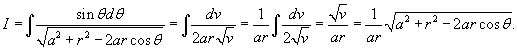 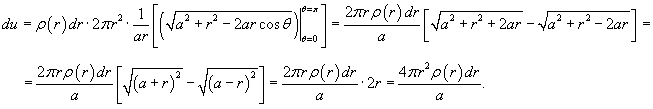 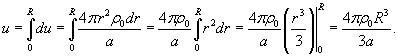 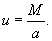 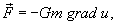 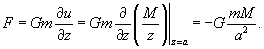 Как видно, сила притяжения шара и точки имеет такой же вид, как и сила притяжения двух точечных масс! Это один из фундаментальных результатов в астрофизике и небесной механике. Благодаря этому, планеты и звезды часто можно рассматривать как материальные точки при описании их движения. Чтобы получить этот результат, Исаак Ньютон был вынужден даже отложить публикацию своих знаменитых "Начал Философии". Возможно трудности были связаны с тем, что он не использовал сферические координаты при решении этой задачи... |
||||||
|
Пример 6
|
||||||
|
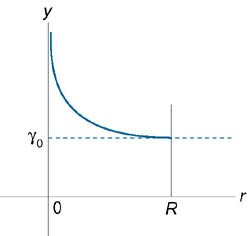
Пусть планета имеет радиус R, а ее плотность выражается зависимостью
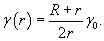 Решение. 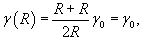
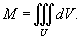 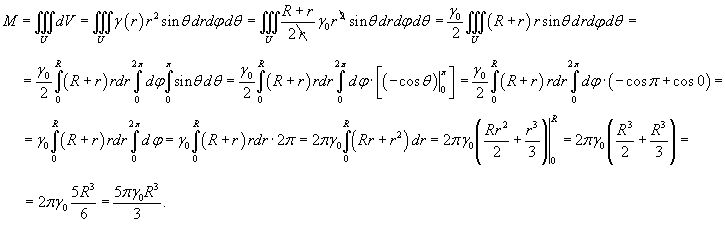 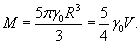 |
||||||