|
Физические приложения поверхностных интегралов
|
||||||
|
Поверхностные интегралы применяются во многих прикладных расчетах. В частности, с их помощью вычисляются
Масса оболочки
Пусть S представляет собой тонкую гладкую оболочку. Распределение массы оболочки описывается функцией плотности 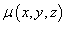 . Тогда полная масса оболочки выражается через поверхностный интеграл первого рода по формуле . Тогда полная масса оболочки выражается через поверхностный интеграл первого рода по формуле

Центр масс и моменты инерции оболочки
Пусть распределение массы m в тонкой оболочке описывается непрерывной функцией плотности 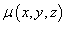 . Координаты центра масс оболочки определяются формулами . Координаты центра масс оболочки определяются формулами
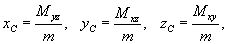 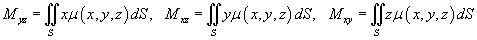 Моменты инерции оболочки относительно осей Ox, Oy, Oz выражаются, соответственно, формулами 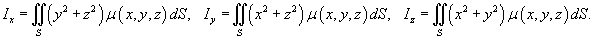 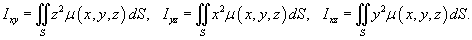
Сила притяжения поверхности
Пусть задана поверхность S, а в точке
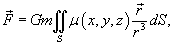 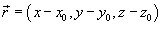 , G - гравитационная постоянная, , G - гравитационная постоянная, 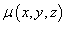 − функция плотности. − функция плотности.
Сила давления
Предположим, что поверхность S задана вектором 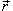 и находится под воздействием некоторой силы давления (это может быть плотина, крыло самолета, стенка баллона со сжатым газом и т.д.). Полная сила и находится под воздействием некоторой силы давления (это может быть плотина, крыло самолета, стенка баллона со сжатым газом и т.д.). Полная сила 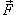 , созданная давлением , созданная давлением 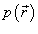 , находится с помощью поверхностного интеграла по формуле , находится с помощью поверхностного интеграла по формуле
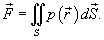 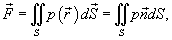 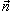 − единичный нормальный вектор к поверхности S. − единичный нормальный вектор к поверхности S.
Поток жидкости и поток вещества
Если в качестве векторного поля рассматривается скорость жидкости 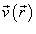 , то поток через поверхность S называется потоком жидкости. Он равен объему жидкости, проходящей через поверхность S в единицу времени и выражается формулой , то поток через поверхность S называется потоком жидкости. Он равен объему жидкости, проходящей через поверхность S в единицу времени и выражается формулой
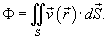 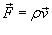 , где ρ − плотность, называется потоком вещества и определяется выражением , где ρ − плотность, называется потоком вещества и определяется выражением
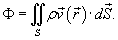
Заряд поверхности
Пусть величина 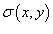 является плотностью распределения заряда по поверхности. Тогда полный заряд, распределенный по проводящей поверхности S выражается формулой является плотностью распределения заряда по поверхности. Тогда полный заряд, распределенный по проводящей поверхности S выражается формулой
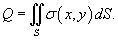
Теорема Гаусса
Поток электрического смещения 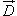 через замкнутую поверхность S равен алгебраической сумме всех зарядов, расположенных внутри поверхности: через замкнутую поверхность S равен алгебраической сумме всех зарядов, расположенных внутри поверхности:
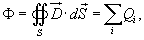 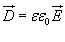 , , 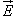 − напряженность электрического поля, ε − относительная диэлектрическая проницаемость среды, − напряженность электрического поля, ε − относительная диэлектрическая проницаемость среды, 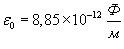 − диэлектрическая проницаемость вакуума. − диэлектрическая проницаемость вакуума.Теорема Гаусса применима к любым замкнутым поверхностям. В случае поверхности с достаточной симметрией, данная теорема упрощает вычисление электрического поля. Теорему Гаусса рассматривают как один из основных постулатов теории электричества. Она входит в систему основных уравнений Максвелла. |
||||||
|
Пример 1
|
||||||
|
Найти массу цилиндрической оболочки, заданной параметрически в виде
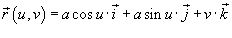 , где , где 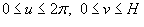 (рисунок 2 выше). Плотность оболочки определяется функцией (рисунок 2 выше). Плотность оболочки определяется функцией 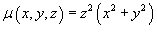 . .
Решение.  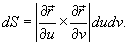 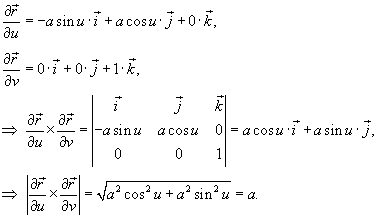 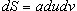 . Следовательно, масса оболочки равна . Следовательно, масса оболочки равна
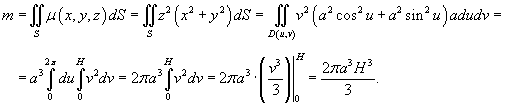 |
||||||
|
Пример 2
|
||||||
|
Найти массу параболической оболочки, заданной уравнением
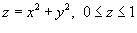 и имеющей плотность и имеющей плотность 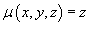 . .
Решение.  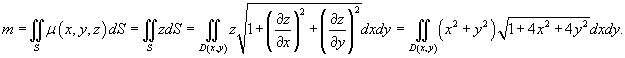 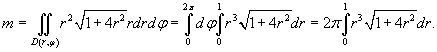 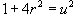 . Тогда . Тогда 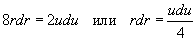 . Здесь . Здесь 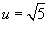 при при 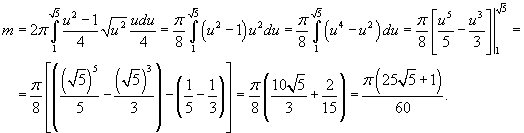 |
||||||
|
Пример 3
|
||||||
|
Найти центр масс части сферической оболочки
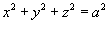 , расположенной в первом октанте и имеющей постоянную плотность μ0. , расположенной в первом октанте и имеющей постоянную плотность μ0.
Решение. 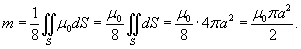
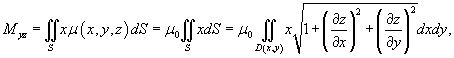 Поскольку 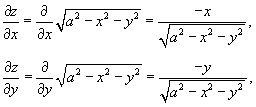 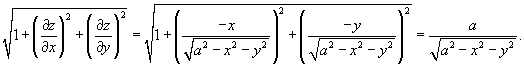 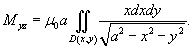 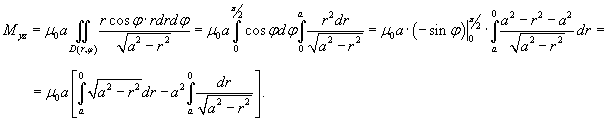 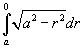 в квадратных скобках. Сделаем замену: в квадратных скобках. Сделаем замену: 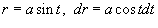 . При . При 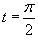 . Тогда интеграл будет равен . Тогда интеграл будет равен
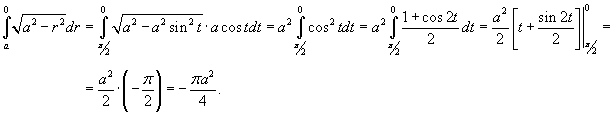 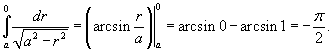 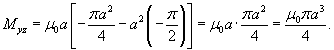 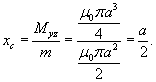 Итак, координаты центра масс оболочки имеют вид 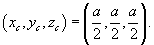 |
||||||
|
Пример 4
|
||||||
|
Вычислить момент инерции однородной сферической оболочки
Решение. 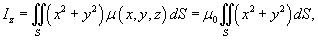 Поскольку поверхность верхней полусферы описывается функцией 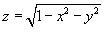 , то элемент площади равен , то элемент площади равен
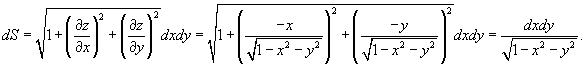 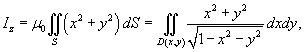 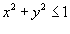 . Переходя к полярным координатам, получаем FIX . Переходя к полярным координатам, получаем FIX
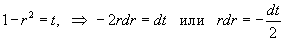 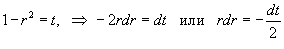 . Если . Если 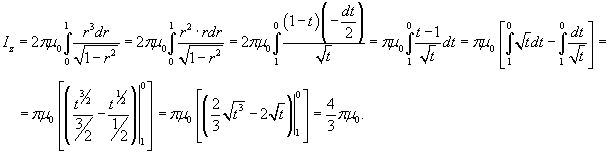 |
||||||
|
Пример 5
|
||||||
|
Найти силу притяжения между полусферой с постоянной плотностью μ0 радиусом r с центром в начале координат и точечной массой m, расположенной в начале координат.
Решение. 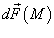 между элементом поверхности dS и массой m можно записать в виде между элементом поверхности dS и массой m можно записать в виде
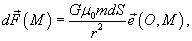 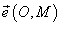 − единичный вектор, направленный из точки O в точку M. − единичный вектор, направленный из точки O в точку M.Так как 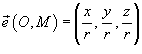 , то можно записать , то можно записать
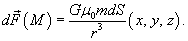 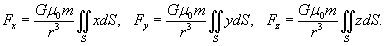 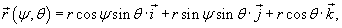 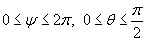 . .Известно, что элемент площади для сферы равен 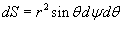 . Тогда компоненты силы притяжения будут равны . Тогда компоненты силы притяжения будут равны
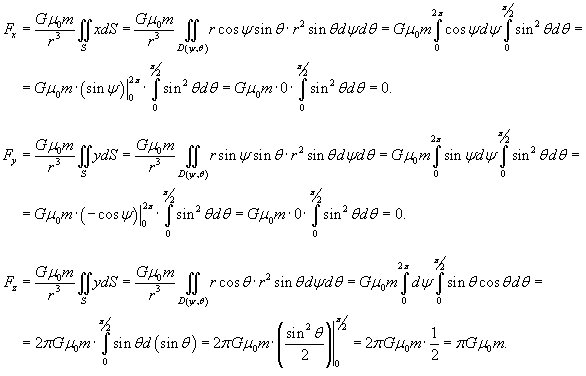 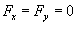 очевиден вследствие симметрии и однородности поверхности. Поэтому, результирующая сила очевиден вследствие симметрии и однородности поверхности. Поэтому, результирующая сила 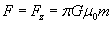 направлена вдоль оси Oz. направлена вдоль оси Oz.
|
||||||
|
Пример 6
|
||||||
|
Оценить силу давления, действующую на дамбу, схематически показанную на рисунке 6 и представляющую собой резервуар воды шириной W и высотой H.
Решение. 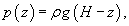 Полная сила давления, действующая на плотину, будет равна 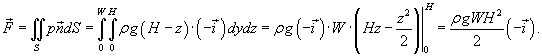 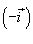 показывает направление действия силы показывает направление действия силы 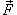 . Абсолютное значение силы равно . Абсолютное значение силы равно
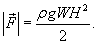 |
||||||
|
Пример 7
|
||||||
|
Вязкая жидкость течет в цилиндрической трубе радиусом R со скоростью
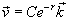 (м·с−1), где (м·с−1), где 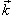 − единичный вектор, направленный вдоль оси трубы в сторону потока, r − расстояние от оси, C − некоторая константа (рисунок 7). Вычислить поток жидкости через поперечное сечение трубы. − единичный вектор, направленный вдоль оси трубы в сторону потока, r − расстояние от оси, C − некоторая константа (рисунок 7). Вычислить поток жидкости через поперечное сечение трубы.
Решение. 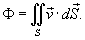 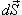 и и 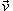 сонаправлены, то поток равен сонаправлены, то поток равен
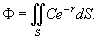 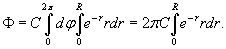 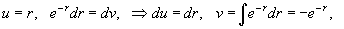 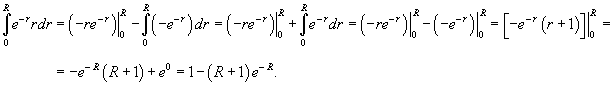 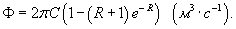
|
||||||
|
Пример 8
|
||||||
|
Определить электрическое поле бесконечной пластины с однородно распределенным зарядом плотностью σ.
Решение. Рассмотрим условную гауссовскую поверхность в форме цилиндра с поперечным сечением S и высотой 2H (рисунок 8). Поток электрического смещения отличен от нуля лишь на основаниях цилиндра. Следовательно, 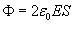 , где E − электрическое поле в основаниях цилиндра. Полный заряд внутри цилиндрической поверхности равен , где E − электрическое поле в основаниях цилиндра. Полный заряд внутри цилиндрической поверхности равен 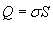 . Тогда по теореме Гаусса получаем . Тогда по теореме Гаусса получаем
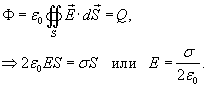 |
||||||







