|
Физические приложения криволинейных интегралов
|
||||||||||||
|
С помощью криволинейных интегралов вычисляются
Масса кривой
Предположим, что кусок проволоки описывается некоторой пространственной кривой C. Пусть масса распределена вдоль этой кривой с плотностью 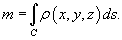 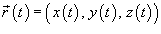 , то ее масса описывается формулой , то ее масса описывается формулой
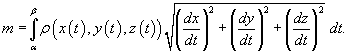 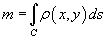 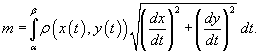
Центр масс и моменты инерции кривой
Пусть снова кусок проволоки описывается некоторой кривой C, а распределение массы вдоль кривой задано непрерывной функцией плотности 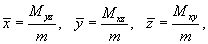 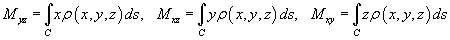 Моменты инерции относительно осей Ox, Oy и Oz определяются формулами 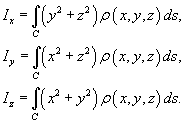
Работа поля
Работа при перемещении тела в силовом поле 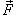 вдоль кривой C выражается через криволинейный интеграл второго рода вдоль кривой C выражается через криволинейный интеграл второго рода
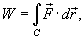 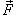 − сила, действующая на тело, − сила, действующая на тело, 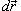 − единичный касательный вектор (рисунок 1). Обозначение − единичный касательный вектор (рисунок 1). Обозначение 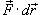 означает скалярное произведение векторов означает скалярное произведение векторов  и и  . .Заметим, что силовое поле  не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы 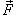 иногда может оказаться отрицательной. иногда может оказаться отрицательной.Если векторное поля задано в координатной форме в виде 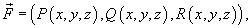 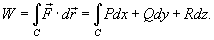 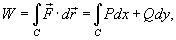 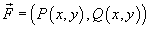 . .Если траектория движения C определена через параметр t (t часто означает время), то формула для вычисления работы принимает вид 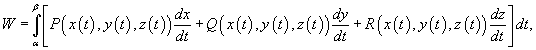 Если векторное поле 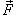 потенциально, то работа по перемещению тела из точки A в точку B выражается формулой потенциально, то работа по перемещению тела из точки A в точку B выражается формулой
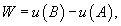 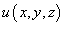 − потенциал поля. − потенциал поля.
Закон Ампера
Криволинейный интеграл от магнитного поля с индукцией 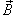 вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой
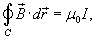 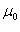 - магнитная проницаемость ваккуума, равная - магнитная проницаемость ваккуума, равная 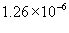 Н/м. Н/м.
Закон Фарадея
Электродвижущая сила ε, наведенная в замкнутом контуре C, равна скорости изменения магнитного потока ψ, проходящего через данный контур (рисунок 3).
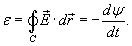
|
||||||||||||
|
Пример 1
|
||||||||||||
|
Определить массу проволоки, имеющей форму отрезка от точки
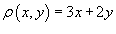 . .
Решение. 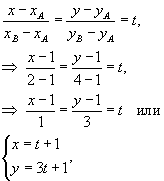 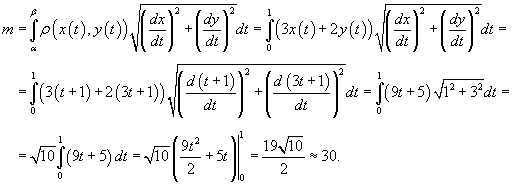 |
||||||||||||
|
Пример 2
|
||||||||||||
|
Определить массу проволоки, имеющей форму дуги окружности
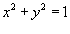 от точки от точки 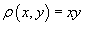 (рисунок 4). (рисунок 4).
Решение. 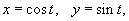 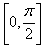 . Тогда масса данного куска проволоки вычисляется следующим образом: . Тогда масса данного куска проволоки вычисляется следующим образом:
|
||||||||||||
|
Пример 3
|
||||||||||||
|
Найти центр масс проволоки, имеющей форму кардиоиды
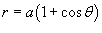 (рисунок 5), где с плотностью (рисунок 5), где с плотностью Решение.  . Чтобы найти координату центра масс . Чтобы найти координату центра масс 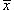 , достаточно рассмотреть верхнюю половину кардиоиды. , достаточно рассмотреть верхнюю половину кардиоиды.Предварительно найдем полную массу кардиоиды. В полярных координатах получаем  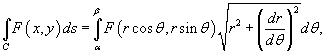 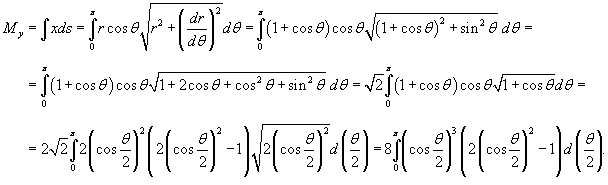 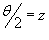 (нижний и верхний пределы интегрирования становятся равными, соответственно, 0 и (нижний и верхний пределы интегрирования становятся равными, соответственно, 0 и 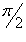 ), можно записать ), можно записать
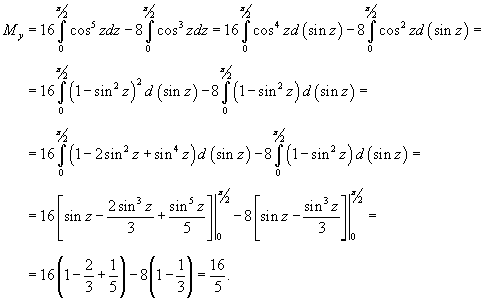 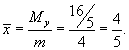 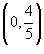 . . |
||||||||||||
|
Пример 4
|
||||||||||||
|
Вычислить момент инерции Ix проволоки в форме окружности
Решение. 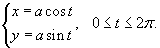 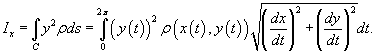 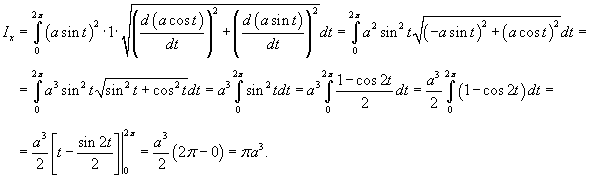 |
||||||||||||
|
Пример 5
|
||||||||||||
|
Найти работу, совершаемую полем
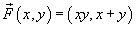 при перемещении тела от начала координат при перемещении тела от начала координат 1) С − отрезок прямой 2) С − кривая 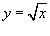 . .
Решение. 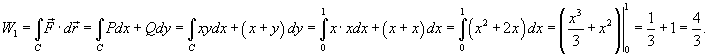 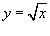 . .
 |
||||||||||||
|
Пример 6
|
||||||||||||
|
Тело массой m брошено под углом к горизонту α с начальной скоростью v0 (рисунок 6). Вычислить работу силы притяжения
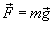 за время движения тела до момента соударения с землей. за время движения тела до момента соударения с землей.
Решение. 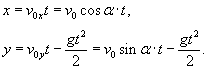 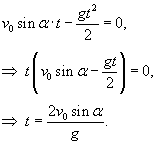 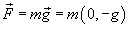 . Тогда работа за время перемещения тела равна . Тогда работа за время перемещения тела равна
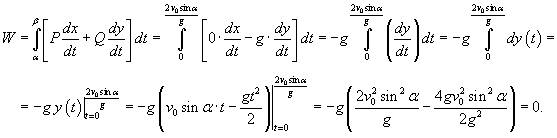 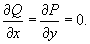 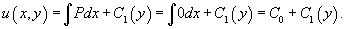 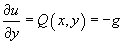 , находим , находим
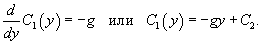 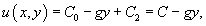 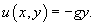 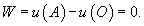
|
||||||||||||
|
Пример 7
|
||||||||||||
|
Вычислить индукцию магнитного поля в вакууме на расстоянии r от оси бесконечно длинного проводника с током I.
Решение. 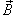 направлено по касательной к круговому контуру в любой его точке, то скалярное произведение векторов направлено по касательной к круговому контуру в любой его точке, то скалярное произведение векторов 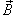 и и 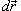 есть просто есть просто 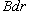 . Тогда можно записать . Тогда можно записать
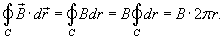 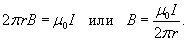 |
||||||||||||
|
Пример 8
|
||||||||||||
|
Оценить значение электродвижущей силы ε и электрического поля E, возникающих в кольце радиусом
Решение. 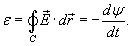 Предположим, что магнитное поле  перпендикулярно плоскости кольца. Тогда за время перпендикулярно плоскости кольца. Тогда за время 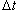 изменение потока равно изменение потока равно
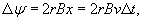 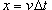 , v − скорость самолета, B − индукция магнитного поля Земли. Из последнего выражения получаем , v − скорость самолета, B − индукция магнитного поля Земли. Из последнего выражения получаем
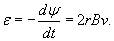 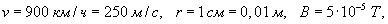 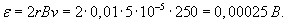 Напряженность возникающего электрического поля найдем по формуле 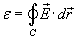 . В силу симметрии, наведенное электрическое поле будет иметь постоянную амплитуду в любой точке кольца. Оно будет направлено по касательной к кольцу в любой его точке. Это позволяет легко вычислить криволинейный интеграл. . В силу симметрии, наведенное электрическое поле будет иметь постоянную амплитуду в любой точке кольца. Оно будет направлено по касательной к кольцу в любой его точке. Это позволяет легко вычислить криволинейный интеграл.
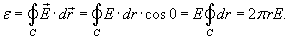 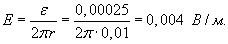 |
||||||||||||






