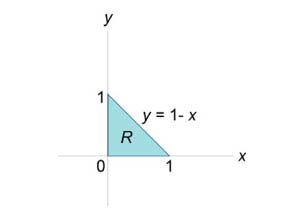|
Физические приложения двойных интегралов
|
||||||
|
Масса и статические моменты пластины
Предположим, что плоская пластина изготовлена из неоднородного материала и занимает область R в плоскости Oxy. Пусть плотность пластины в точке 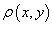 . Тогда масса пластины выражается через двойной интеграл в виде . Тогда масса пластины выражается через двойной интеграл в виде
 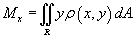 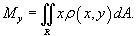 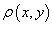 , описываются формулами , описываются формулами
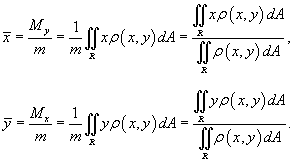 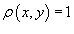 для всех для всех
Моменты инерции пластины
Момент инерции пластины относительно оси 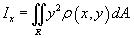 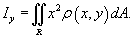 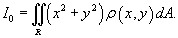
Заряд пластины
Предположим, что электрический заряд распределен по области R в плоскости Oxy и его плотность распределения задана функцией 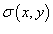 . Тогда полный заряд пластины Q определяется выражением . Тогда полный заряд пластины Q определяется выражением
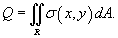
Среднее значение функции
Приведем также формулу дял расчета среднего значения некоторой распределенной величины. Пусть 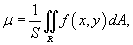 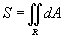 − площадь области интегрирования R. − площадь области интегрирования R. |
||||||
|
Пример 1
|
||||||
|
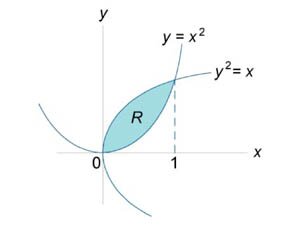
Определить координаты центра тяжести однородной пластины, образованной параболами
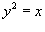 и и 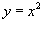 . .
Решение. 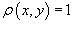 . Тогда масса пластины равна . Тогда масса пластины равна
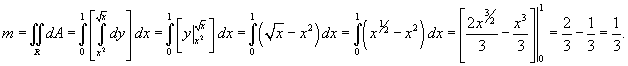 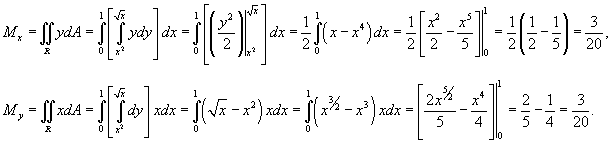 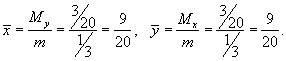
|
||||||
|
Пример 2
|
||||||
|
Вычислить моменты инерции треугольника, ограниченного прямыми
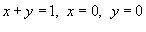 (рисунок 2) и имеющего плотность (рисунок 2) и имеющего плотность  . .
Решение. 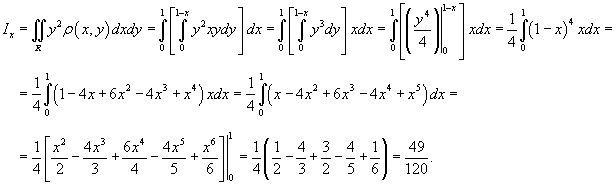 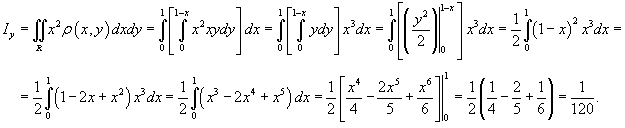 |
||||||
|
Пример 3
|
||||||
|
Электрический заряд по площади диска
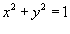 таким образом, что его поверхностная плотность равна таким образом, что его поверхностная плотность равна 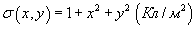 . Вычислить полный заряд диска. . Вычислить полный заряд диска.
Решение. 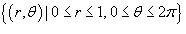 . Полный заряд будет равен . Полный заряд будет равен
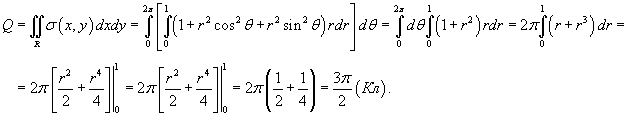 |
||||||