|
Ортогональные полиномы и обобщенный ряд Фурье
|
||||||
|
Ортогональные полиномы
Два полинома, заданные на интервале 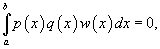 Множество полиномов 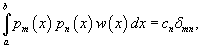
Обобщенный ряд Фурье
Обобщенным рядом Фурье для некоторой функции называется ее разложение в ряд на основе системы ортогональных полиномов. Любая кусочно непрерывная функция может быть представлена в виде обобщенного ряда Фурье:
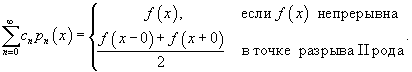
Полиномы Эрмита
Полиномы Эрмита ортогональны с весовой функцией 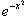 на интервале на интервале 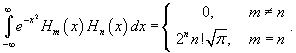 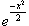 . Это соглашение распространено в теории вероятностей, в частности, из-за того, что плотность нормального распределения описывается функцией . Это соглашение распространено в теории вероятностей, в частности, из-за того, что плотность нормального распределения описывается функцией 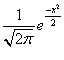 . .
Полиномы Лагерра
Полиномы Лагерра 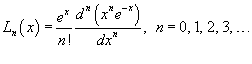 ортогональны с весовой функцией ортогональны с весовой функцией 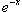 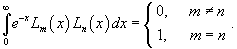
Полиномы Лежандра
Полиномы Лежандра 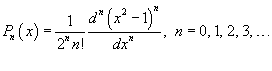 ортогональны на интервале ортогональны на интервале 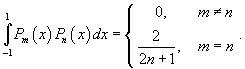
Полиномы Чебышева
Полиномы Чебышева 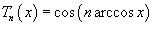 первого рода ортогональны на отрезке первого рода ортогональны на отрезке 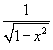 : :
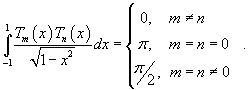 |
||||||
|
Пример 1
|
||||||
|
Показать, что множество функций
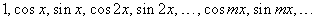 Решение. 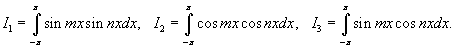 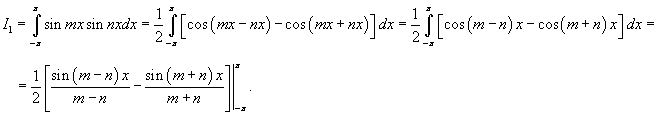 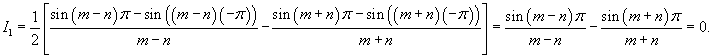 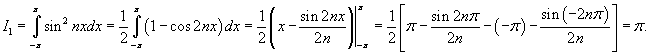 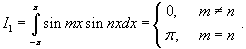 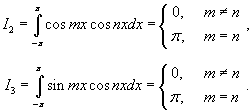 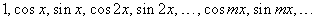 |
||||||
|
Пример 2
|
||||||
|
Найти разложение функции
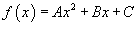 в ряд Фурье-Эрмита. в ряд Фурье-Эрмита.
Решение. 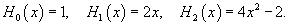 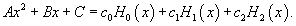 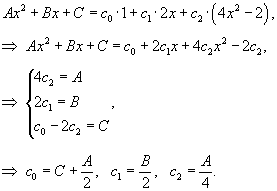 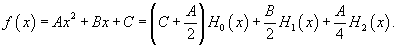 |
||||||
|
Пример 3
|
||||||
|
Найти разложение степенной функции
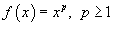 в ряд Фурье-Лагерра. в ряд Фурье-Лагерра.
Решение. 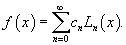 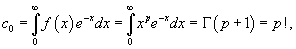 Для 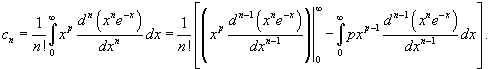 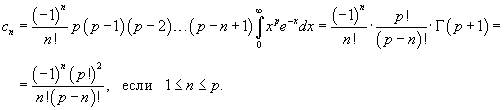 Следовательно, разложение степенной функции 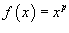 в ряд Фурье-Лагерра имеет вид: в ряд Фурье-Лагерра имеет вид:
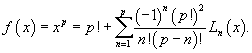 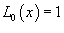 , то решение можно записать в более компактной форме: , то решение можно записать в более компактной форме:
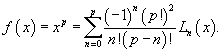 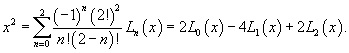 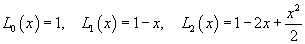 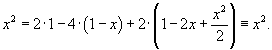 |
||||||
|
Пример 4
|
||||||
|
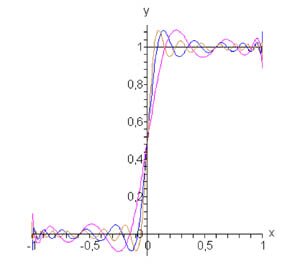
Найти разложение в ряд Фурье-Лежандра ступенчатой функции
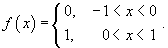 Решение. 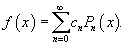  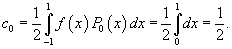 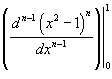 , чтобы найти ы cn при , чтобы найти ы cn при 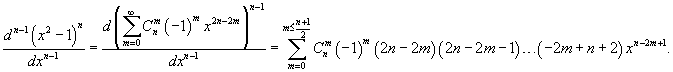 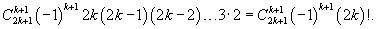  при при 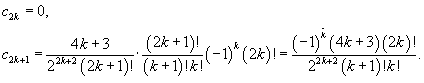 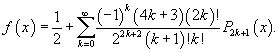
|
||||||
|
Пример 5
|
||||||
|
Найти разложение функции
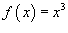 в ряд Фурье-Чебышева на интервале в ряд Фурье-Чебышева на интервале Решение. 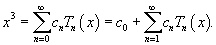 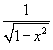 . .Умножая обе части последнего равенства на 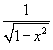 и интегрируя на отрезке и интегрируя на отрезке 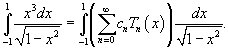 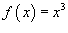 нечетная, и мы интегрируем на симметричном интервале нечетная, и мы интегрируем на симметричном интервале 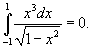 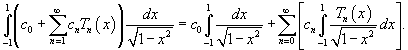 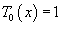 , видим, что , видим, что
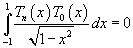 Таким образом, 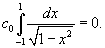 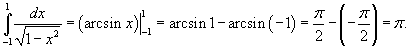 Аналогично можно определить ы cn. Умножим выражение 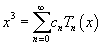 на на 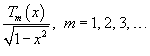 и проинтегрируем его от −1 до 1. Получаем и проинтегрируем его от −1 до 1. Получаем
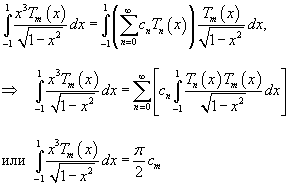 Подставим далее явные выражения для 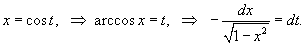
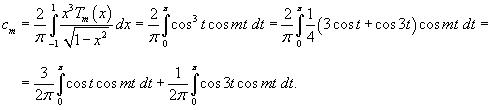 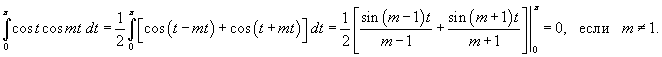 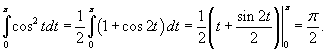 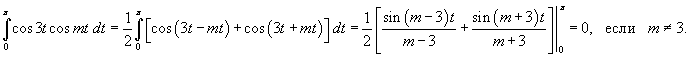 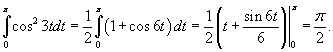 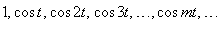 ортогонально на интервале ортогонально на интервале 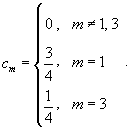 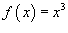 на интервале на интервале 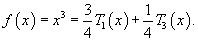 |
||||||