Экономические задачи на оптимизацию

Приведенные ниже задачи описывают разнообразные ситуации, с которыми корпорации и компании могут встретиться в своей экономической деятельности. В каждой из этих задач необходимо построить функцию, устанавливающую связь между двумя экономическими величинами (например, между объемом производства и прибылью компании), и исследовать ее на экстремальное значение. Задачи на оптимизацию такого типа эффективно решаются с использованием производной.

   Пример 1

Завод изготавливает и продает полупроводниковые приборы. Удельные расходы (в расчете на один прибор) зависят от объема производства и включают в себя постоянную часть в размере 1000 (руб/прибор) и переменную часть 2n (руб/прибор), где n − число приборов, изготовленных за месяц. Цена прибора, в свою очередь, зависит от объема производства по закону  p(n) = 10000 − n  (руб/прибор). Определить, при каком объеме производства прибыль будет максимальной? Доход от продажи приборов, изготовленных в течение месяца, равен Месячные расходы при этом составляют Тогда прибыль определяется формулой Исследуем функцию прибыли на экстремум. При этом будем считать, что n является действительным числом. Дифференцируя по n, получаем: Вычислим также вторую производную: Поскольку вторая производная всюду отрицательна, то решение n = 1500 является точкой максимума, то есть при производстве 1500 приборов в месяц прибыль предприятия будет максимальной.

   Пример 2

На изготовление x единиц товара фирма затрачивает где a и b − некоторые действительные числа. Товар продается по цене p рублей за штуку. Определить объем продаж, при котором прибыль будет наибольшей. При продаже x единиц товара фмрма получаем доход, равный Следовательно, прибыль фирмы составляет Найдем производную функции P(x): Производная равна нулю в точке Рассмотрим вторую производную: Так как вторая производная отрицательна, то точка x = (p − b)/(2a) является точкой максимума, т.е. при данном объеме продаж прибыль фирмы будет наибольшей.

   Пример 3

Компания продает товар по цене 100 рублей, если объем партии не превышает 5000 единиц. При большем объеме предоставляется скидка в размере 5 рублей на каждую последующую тысячу, превышающую уровень 5000. При каком объеме заказа компания получаем наибольший доход? Обозначим количество товара в партии через x. Если x ≤ 5000, то цена единицы товара по условию составляет 100 рублей. Если же x > 5000, то цена вычисляется по формуле В первом случае, при x ≤ 5000, максимальный доход достигается при x = 5000. Он равен Во втором случае, при x > 5000, доход определяется следующей функцией: Находим производную: Приравнивая ее нулю, определяем критическую точку: Заметим, что вторая производная функции R(x) всегда отрицательна: Поэтому найденная критическая точка соответствует максимуму функции R(x). Таким образом, доход компании будет максимальным при продаже партии товаров x = 12500 единиц. Максимальный доход при этом составит

   Пример 4

В некотором государстве используется прогрессивная система налогообложения. Сумма налога состоит из линейной части, пропорциональной доходу, и нелинейной части, зависящей от дохода по степенному закону. Общая величина налога определяется формулой где W − доход, p − показатель степени, a, b, c − положительные коэффициенты. При каком уровне дохода ставка налога будет минимальной? Налоговая ставка r вычисляется по формуле Исследуем ее на экстремум. Находим производную: Видно, что функция r(W) имеет три критических точки, но поскольку коэффициенты b, c > 0, то содержательное решение существует лишь в следующей точке: При переходе через это значение производная меняет знак с минуса на плюс, Следовательно, здесь функция r(W) достигает минимума, т.е. налоговая ставка при этом уровне дохода будет наименьшей.

   Пример 5

Компания изготавливает и продает 1000 изделий в месяц по цене 2000 рублей за штуку. При уменьшении цены на 50 рублей можно дополнительно продать еще 50 изделий в месяц. При какой цене фирма получит максимальный доход и каково его значение? Обозначим через x количество вычетов по 50 рублей из базовой цены 2000 рублей. Тогда цена одного изделия (при продаже более 1000 изделий в месяц) равна 2000 − 50x. Общее количество проданных изделий будет составлять 1000 + 50x  штук. Полный доход описывается выражением Дифференцируя функцию R(x), найдем точку экстремума: Заметим, что вторая производная функции R(x) отрицательна: Поэтому x = 10 является точкой максимума. Следовательно, доход будет наибольшим, когда число вычетов равно x = 10. Цена изделия в этом случае составляет а объем продаж за месяц равен Соответственно, максимальный доход компании составляет

   Пример 6

При плавании корабля расходы на топливо пропорциональны квадрату его скорости. Кроме этого существуют постоянные расходы, не зависящие от скорости и составляющие p (рублей/час). При какой скорости общие расходы на 1 км пути будут наименьшими? По условию задачи, переменная часть расходов зависит от скорости следующим образом: где k − коэффициент пропорциональности. Тогда суммарные расходы за один час выражаются формулой За один час корабль проходит расстояние, равное v. Поэтому расходы на 1 км пути составляют Полученное выражение представляет собой функцию от скорости v. Исследуем ее на экстремум: При найденном значении v функция C₁(v) достигает минимума, так как производная при переходе через эту точку меняет знак с минуса на плюс. Следовательно, при такой скорости расходы на 1 км пути будут наименьшими. Сумма расходов за 1 час при этом составляет т.е. равна удвоенным постоянным расходам.

   Пример 7

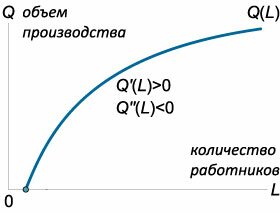
Зависимость объема производства Q от количества работников L описывается функцией Q(L) (рисунок 1). Показать, что если производные удовлетворяют условиям то существует оптимальное число работников L*, при котором прибыль будет наибольшей. Условия Q'(L) > 0, Q''(L) < 0 отражают снижение производительности труда при увеличении числа работников и часто встречаются на практике. Полагая, что расходы, связанные с работниками, пропорциональны их количеству, можно записать выражение для прибыли в виде где p − цена продажи единицы продукции, Q(L) − рассмотренный выше объем производства, qL − часть расходов, связанная с работниками, C − постоянная часть расходов, не зависящая от числа работников.

В данной формуле pQ(L) выражает доход предприятия за определенный период. В результате прибыль P представляет собой функцию от числа работников P(L).

Исследуем возможный экстремум этой функции. Первая производная имеет вид: Функция прибыли P(L) имеет критическую точку L* при условии Поскольку вторая производная отрицательна при всех допустимых значениях L, то критическая точка является точкой максимума. Таким образом, в заданной системе всегда существует оптимальное количество работников L*, при котором прибыль предприятия максимальна.

   Пример 8

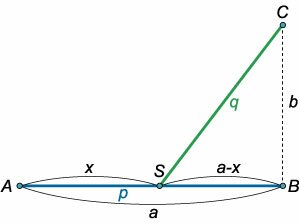
Города A и B находятся на расстоянии a км и соединены прямой железной дорогой. Для перевозки грузов из города A в город C, отстоящий от железной дороги на b км, необходимо построить автомобильную дорогу, примыкающую к железной дороге (рисунок 2). К какой точке S следует провести шоссе, чтобы транспортировка грузов была наиболее экономичной? Стоимость перевозки 1 тонны груза на 1 км составляет p руб. по железной дороге и q руб. по автомобильной дороге. Обозначим через x расстояние от города A до автомобильного съезда S. Тогда стоимость перевозки 1 тонны груза по железнодорожному участку AS равна px. Длина автомобильного участка пути SC определяется по теореме Пифагора и составляет Соответственно, стоимость перевозки по этому автомобильному участку будет равна Следовательно, полная стоимость транспортировки 1 тонны груза из пункта A в пункт C описывается функцией Для исследования экстремальных значений функции Q(x), найдем ee производную: Приравнивая производную нулю, вычисляем критическое значение x: Посмотрим как изменяется знак производной при переходе через найденное критическое значение. В выражении для производной в виде числитель дроби при уменьшении или увеличении x изменяется больше, чем знаменатель. Поэтому в левой окрестности критической точки производная будет отрицательной, а в правой окрестности − положительной. Таким образом, данная точка соответствует минимуму функции Q(x).

Заметим, что найденное решение является действительным лишь при условии q > p, т.е. удельные расходы по перевозке грузов по автомобильной дороге должны превышать расходы при транспортировке по железной дороге. Это условие, однако, не является единственным ограничением на возможные значения p и q. Исследуя диапазон значений, в котором может изменяться отношение q/p, рассмотрим два предельных случая:

Если x = 0, то получаем следующее решение: Это отношение удельных расходов q/p является минимально возможным. При этом значении q/p надо строить автомобильную дорогу сразу вдоль диагонали AC.

Другой предельный случай соответствует решению x = a: Здесь отношение q/p стремится к бесконечности. Ясно, что на практике указанное отношение является конечным, т.е. оптимальная точка ответвления всегда будет находиться в промежутке 0 ≤ x < a.