|
Нелинейный математический маятник
|
||||||
|
Дифференциальное уравнение колебаний
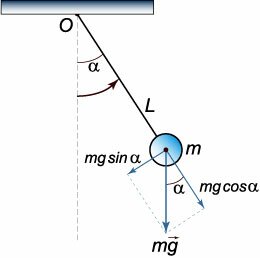
Математический маятник представляет собой идеальную модель, в которой материальная точка массой m подвешена на невесомой и нерастяжимой нити длиной L. В такой системе происходят периодические колебания, которые можно рассматривать как вращение маятника вокруг оси O (рисунок 1).
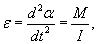 В нашем случае момент силы определяется проекцией силы тяжести на тангенциальное направление, т.е. 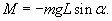 Момент инерции маятника выражается формулой 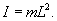 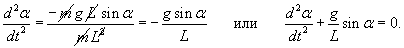  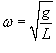 − круговая частота колебаний. − круговая частота колебаний.Период малых колебаний маятника описывается известной формулой 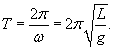
Период колебаний нелинейного математического маятника
Итак, пусть маятник описывается нелинейным дифференциальным уравнением второго порядка
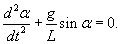 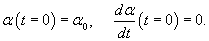 Порядок уравнения можно понизить, если подобрать подходящий интегрирующий множитель. Умножим данное уравнение на интегрирующий множитель 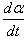 . Это приводит к уравнению . Это приводит к уравнению
 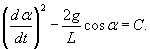 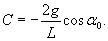 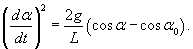 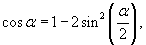 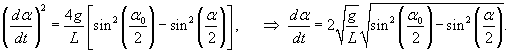 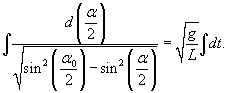 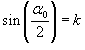 и введем новую переменную θ вместо угла α: и введем новую переменную θ вместо угла α:
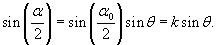 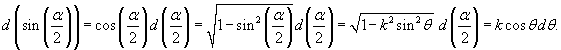 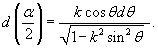 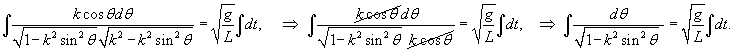  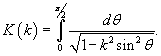 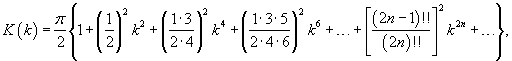 Заметим, что если мы ограничимся нулевым членом разложения, полагая 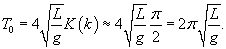 |
||||||
|
Пример
|
||||||
|
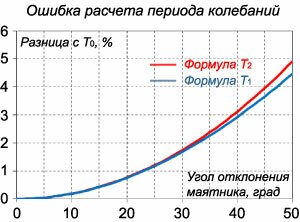
Оценить ошибку в расчете периода колебаний математического маятника в случае использования простейшей формулы T0 = 2π √L/g при различной амплитуде колебаний α0.
Решение. 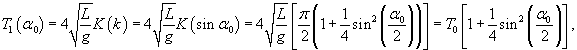 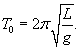 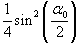 сразу же показывает отклонение от стандартной формулы (в долях единицы) в зависимости от угла α0. сразу же показывает отклонение от стандартной формулы (в долях единицы) в зависимости от угла α0.Аналогичным образом учтем вклад последующих членов ряда при 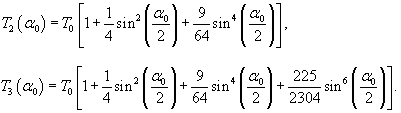
|
||||||