Закон охлаждения Ньютона

В конце 17 века британский ученый Исаак Ньютон изучал охлаждение тел. Эксперименты показали, что скорость охлаждения примерно пропорциональна разнице температур между нагретым телом и окружающей средой. Этот факт можно записать в виде дифференциального уравнения: где Q − количество теплоты, A − площадь поверхности тела, через которую передается тепло, T − температура тела, T_S − температура окружающей среды, α − коэффициент теплопередачи, зависящий от геометрии тела, состояния поверхности, режима теплопередачи и других факторов.

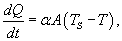Поскольку 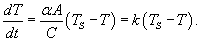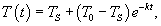Q = CT, где C − теплоемкость тела, то дифференциальное уравнение можно записать как Решение данного уравнение имеет вид: где T₀ обозначает начальную температуру тела.

Таким образом, температура тела уменьшается экспоненциально по мере охлаждения, приближаясь к температуре окружающей среды. Скорость охлаждения зависит от параметра 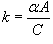(коэффициента теплопроводности). С увеличением коэффициента k (например, вследствие увеличения площади поверхности), тело будет охлаждаться быстрее (рисунок 1.)

   Пример 1

Температура тела уменьшилась с 200^o до 100^o за первый час. Определить на сколько градусов понизится температура еще через один час, если температура окружающей среды 0^o? Мы решим задачу сначала для случая произвольной температуры окружающей среды, а затем вычислим конечную температуру тела при температуре среды 0^o.

Пусть начальная температура нагретого тела составляет 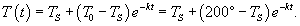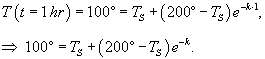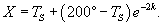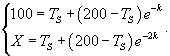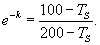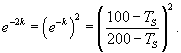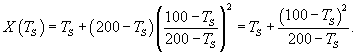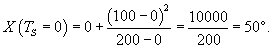T₀ = 200^o. Последующее изменение температуры описывается формулой: В конце первого часа тело охладилось до 100^o. Следовательно, можно записать следующее соотношение: Спустя 2 часа температура тела становится равной X градусов: Таким образом, мы получили систему двух уравнений с тремя неизвестными: T_S, k и X: Мы не можем однозначно определить температуру тела X через 2 часа из данной системы. Однако можно вывести зависимость X от температуры окружающей среды T_S. Выразим функцию e^−k из первого уравнения: Тогда Следовательно, зависимость X(T_S) имеет вид: Если, например, положить температуру окружающей среды равной нулю, то температура тела через два часа будет составлять Зависимость температуры тела X от температуры окружающей среды в данной задаче показана выше на рисунке 2.

   Пример 2

Тело с начальной температурой T₀ помещено в комнату с температурой T_S0 и начинает охлаждаться в соответствии с законом Ньютона с постоянной величиной k. При этом температура комнаты медленно растет по линейному закону где β − известный параметр. Определить момент времени τ, когда температуры тела и окружающей среды сравняются. Прежде всего, отметим разницу со случаем когда тело охлаждается в среде, температура которой постоянна. В этом случае температура тела формально будет бесконечно долго приближаться к температуре окружающей среды. В нашей же задаче температура среды линейно возрастает. Поэтому, рано или поздно температуры тела и среды сравняются, то есть задача имеет решение. Будем считать также, что соблюдается квазистационарный режим, т.е. все переходные процессы в системе быстро затухают.

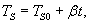В таком случае процесс можно описать дифференциальным уравнением: 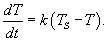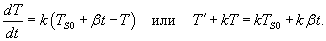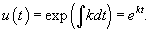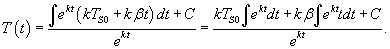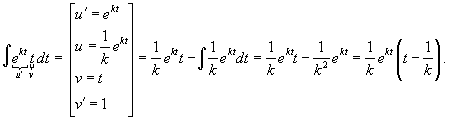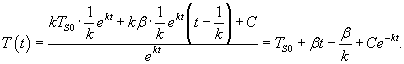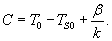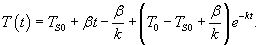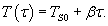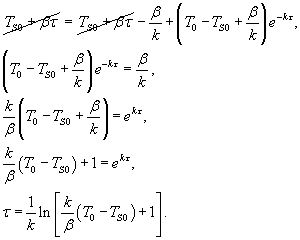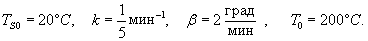По условию задачи, T_S =T_S0 + βt. Следовательно, последнее уравнение можно записать в виде: Мы получили линейное дифференциальное уравнение, которое можно решить, например, с помощью интегрирующего множителя: Общее решение уравнения записыватся в форме Второй интеграл в числителе находится интегрированием по частям: Таким образом, закон охлаждения тела имеет следующий вид: Постоянная C определяется из начального условия T(t = 0) = T₀. Тогда Итак, процесс охлаждения тела описывается формулой В момент τ, температуры тела и окружающей среды становятся равными друг другу: Время τ определяется из уравнения: Мы можем сделать оценку времени τ для некоторых типичных значений параметров: В результате получаем: