|
Натуральный логарифм
|
||||||
|
Логарифм по основанию e (e - трансцендентное число, приближенно равное 2,718281828...) называется натуральным логарифмом. Натуральный логарифм числа x обозначается
Соотношение между логарифмом по основанию a и натуральным логарифмом
Пусть число a является основанием логарифма 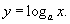 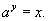 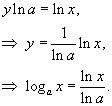 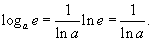 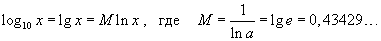 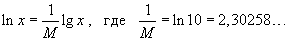
|
||||||
|
Пример 1
|
||||||
|
Вычислить
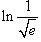 . .
Решение. 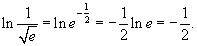 |
||||||
|
Пример 2
|
||||||
|
Записать в виде одного логарифма
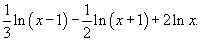 Решение. 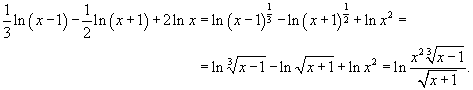 |
||||||
|
Пример 3
|
||||||
|
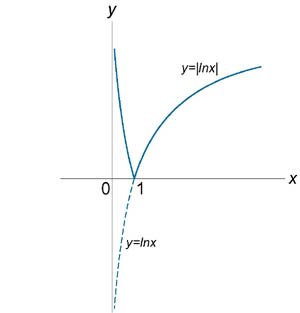
Схематически изобразить график функции
Решение. |
||||||
|
Пример 4
|
||||||
|
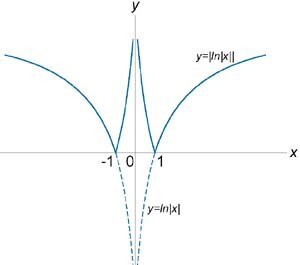
Схематически изобразить график функции
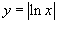 . .
Решение. 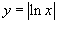 , лежащая в области , лежащая в области
|
||||||
|
Пример 5
|
||||||
|
Схематически изобразить график функции
Решение. |
||||||