|
Метод функций Ляпунова
|
||||||||||||
|
Определение функции Ляпунова
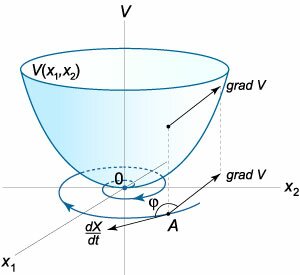
Функция Ляпунова представляет собой скалярную функцию, заданную на фазовом пространстве системы, с помощью которой можно доказать устойчивость положения равновесия. Метод функций Ляпунова применяется для исследования устойчивости различных дифференциальных уравнений и систем. Ниже мы ограничимся рассмотрением автономных систем
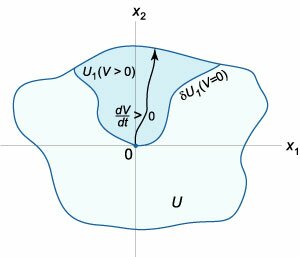
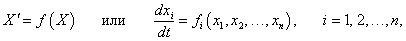 Предположим, что в некоторой окрестности U начала координат задана непрерывно дифференцируемая функция 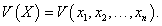 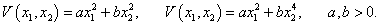 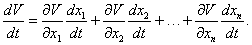 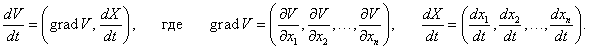 Рассмотрим случай, когда производная функции V(X) в окрестности U начала координат отрицательна: 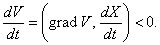
Перейдем к строгим формулировкам. Функция V(X), непрерывно дифференцируемая в некоторой окрестности U начала координат, называется функцией Ляпунова автономной системы 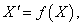
Теоремы об устойчивости
Теорема об устойчивости в смысле Ляпунова. Если в некоторой окрестности U нулевого решения Теорема об асимптотической устойчивости. Если в некоторой окрестности U нулевого решения Как видно, для асимптотической устойчивости нулевого решения требуется, чтобы полная производная dV/dt была строго отрицательной (отрицательно определенной) в окрестности начала координат.
Теоремы о неустойчивости
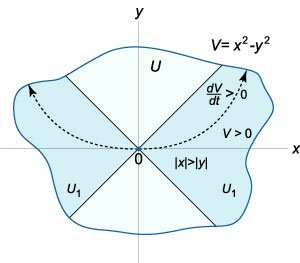
Теорема Ляпунова о неустойчивости. Пусть в окрестности U нулевого решения
Теорема Четаева о неустойчивости. Пусть в окрестности U нулевого решения
Таким образом, функции Ляпунова позволяют установить устойчивость или неустойчивость системы. Преимуществом данного метода является то, что здесь не требуется знать само решение
|
||||||||||||
|
Пример 1
|
||||||||||||
|
Исследовать на устойчивость нулевое решение системы
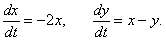
Решение.
Данная система представляет собой линейную однородную систему с постоянными коэффициентами. В качестве функции Ляпунова возьмем квадратичную форму
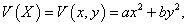 Очевидно, что функция V(x,y) всюду положительна, кроме начала координат, где она равна нулю. Вычислим полную производную функции V(x,y): 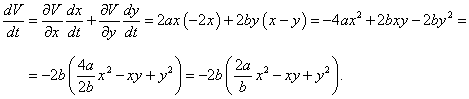 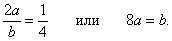 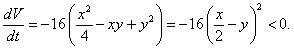 |
||||||||||||
|
Пример 2
|
||||||||||||
|
Исследовать на устойчивость нулевое решение системы
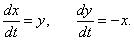
Решение.
Заметим, что для данной системы метод первого приближения неприменим, поскольку нулевое решение представляет собой "центр" (т.е. система не является грубой):
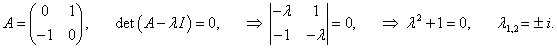 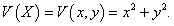 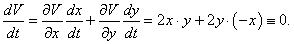 |
||||||||||||
|
Пример 3
|
||||||||||||
|
Исследовать на устойчивость нулевое решение нелинейной системы
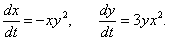
Решение.
Очевидно, что якобиан данной системы в точке (0,0) представляет собой нулевую матрицу:
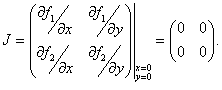 Посмотрим какой результат можно получить, используя функцию Ляпунова. В качестве такой функции возьмем 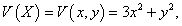 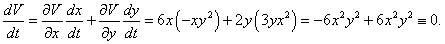 |
||||||||||||
|
Пример 4
|
||||||||||||
|
Исследовать на устойчивость нулевое решение системы, используя метод функций Ляпунова:
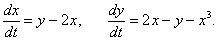
Решение.
В качестве возможной функции Ляпунова выберем функцию вида
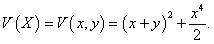 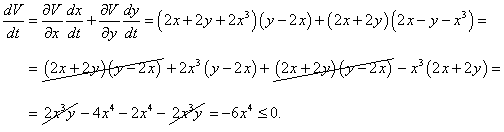 Используя метод первого приближения, можно убедиться, что нулевое положение равновесия представляет собой устойчивый фокус. Действительно, собственные значения линеаризованной системы являются комплексно-сопряженными числами с отрицательной действительной частью: 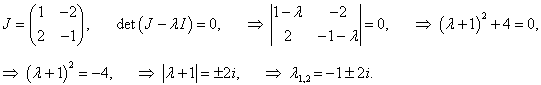 |
||||||||||||
|
Пример 5
|
||||||||||||
|
Используя функцию Ляпунова, исследовать на устойчивость нулевое решение системы

Решение.
Возьмем в качестве функции V(X) следующую функцию:
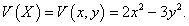  С другой стороны, можно найти точки, сколь угодно близкие к нулю, в которых функция V(X) также будет положительной. Такие точки, например, расположены на оси 0x при Как видно, выполнены условия теоремы Ляпунова о неустойчивости. Следовательно, нулевое решение системы неустойчиво. |
||||||||||||
|
Пример 6
|
||||||||||||
|
Исследовать на устойчивость нулевое решение системы
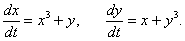
Решение.
Исходя из вида правых частей уравнений, можно заметить, что производные dx/dt, dy/dt будут возрастать для точек в первом квадранте плоскости 0xy (при Пусть функция V(X) имеет вид 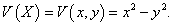 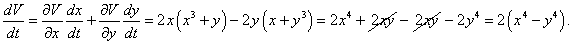 Вычислив собственные значения якобиана линеаризованной системы, можно убедиться, что нулевое положение равновесия является седлом: 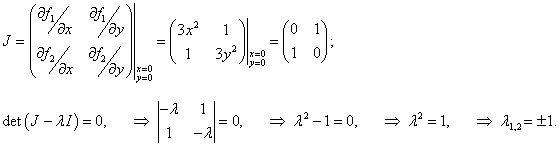 |
||||||||||||