|
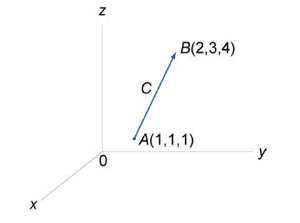
Криволинейные интегралы второго рода
|
||||||
|
Определение
Предположим, что кривая C задана векторной функцией  , где переменная s − длина дуги кривой. Тогда производная векторной функции , где переменная s − длина дуги кривой. Тогда производная векторной функции
 В приведенной выше формуле
 , определенную на кривой C, так, чтобы для скалярной функции , определенную на кривой C, так, чтобы для скалярной функции
  . Такой интеграл . Такой интеграл  называется криволинейным интегралом второго рода от векторной функции называется криволинейным интегралом второго рода от векторной функции  вдоль кривой C и обозначается как вдоль кривой C и обозначается как
   − единичный вектор касательной к кривой C. − единичный вектор касательной к кривой C.Последнюю формулу можно переписать также в векторной форме:   . .Если кривая C лежит в плоскости Oxy, то полагая 
Свойства криволинейного интеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами:
|
||||||
|
Пример 1
|
||||||
|
Вычислить интеграл
 , где кривая C задана параметрически в виде , где кривая C задана параметрически в виде  . .
Решение.   |
||||||
|
Пример 2
|
||||||
|
Найти интеграл
 вдоль кривой C, заданной уравнением вдоль кривой C, заданной уравнением  , от точки (0,0) до (2,8). , от точки (0,0) до (2,8).
Решение.   и и  в подынтегральное выражение, получаем в подынтегральное выражение, получаем
 |
||||||
|
Пример 3
|
||||||
|
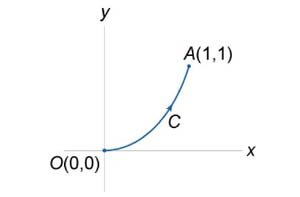
Вычислить
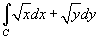 вдоль кривой вдоль кривой 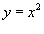 от точки O (0,0) до A (1,1) (рисунок 3 ниже). от точки O (0,0) до A (1,1) (рисунок 3 ниже).
Решение.  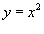 и и 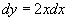 в подынтегральное выражение, находим ответ: в подынтегральное выражение, находим ответ:
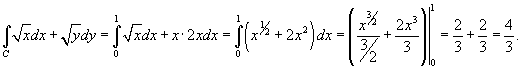 |
||||||
|
Пример 4
|
||||||
|
Вычислить
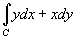 вдоль кривой вдоль кривой 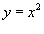 от точки O (0,0) до A (1,1) (рисунок 3). от точки O (0,0) до A (1,1) (рисунок 3).
Решение. 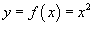 , то по формуле , то по формуле
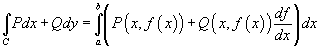 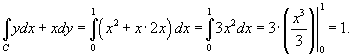
|
||||||
|
Пример 5
|
||||||
|
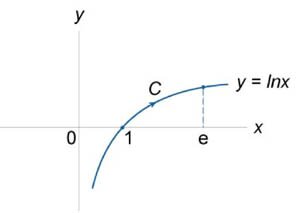
Вычислить криволинейный интеграл
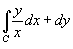 вдоль кривой вдоль кривой 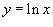 в интервале в интервале 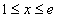 (рисунок 4). (рисунок 4).
Решение. 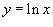 , то дифференциал равен , то дифференциал равен 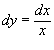 . В соответствии с формулой . В соответствии с формулой
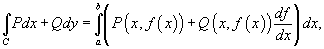 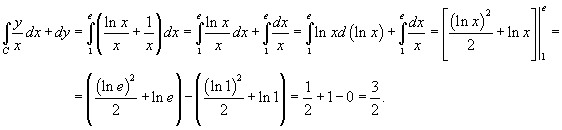 |
||||||
|
Пример 6
|
||||||
|
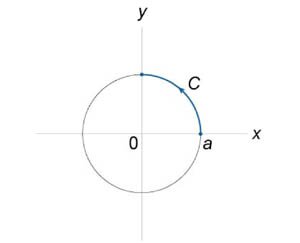
Вычислить криволинейный интеграл
 , где C − дуга окружности, лежащая в первом квадранте, обход которой осуществляется против часовой стрелки (рисунок 5). , где C − дуга окружности, лежащая в первом квадранте, обход которой осуществляется против часовой стрелки (рисунок 5).
Решение. 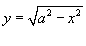 , a − радиус окружности. (Мы взяли положительное значение корня, поскольку , a − радиус окружности. (Мы взяли положительное значение корня, поскольку 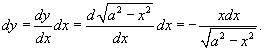 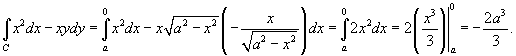
|
||||||
|
Пример 7
|
||||||
|
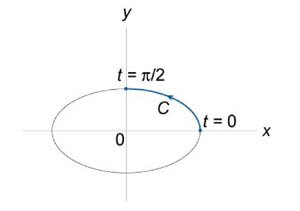
Вычислить криволинейный интеграл
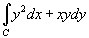 , где C − дуга эллипса (рисунок 6), заданного параметрически в виде , где C − дуга эллипса (рисунок 6), заданного параметрически в виде 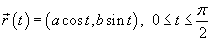 . .
Решение. 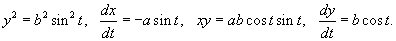 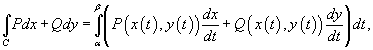 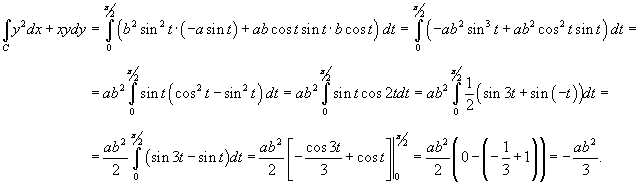 |
||||||
|
Пример 8
|
||||||
|
Найти интеграл
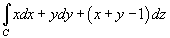 вдоль линии C, представляющей собой отрезок прямой от точки вдоль линии C, представляющей собой отрезок прямой от точки Решение. 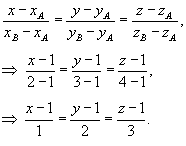 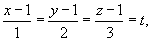 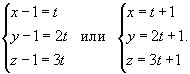  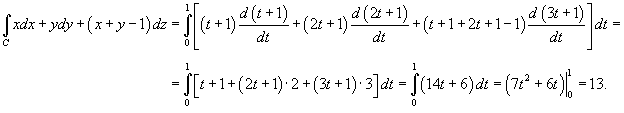
|
||||||




 , то
, то
 (предполагается, что
(предполагается, что