|
Криволинейные интегралы первого рода
|
||||||
|
Определение
Пусть кривая C описывается векторной функцией  , где переменная s представляет собой длину дуги кривой (рисунок 1). , где переменная s представляет собой длину дуги кривой (рисунок 1).Если на кривой C определена скалярная функция F, то интеграл  называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как
  существует, если функция F непрерывна на кривой C. существует, если функция F непрерывна на кривой C.
Свойства криволинейного интеграла первого рода
Криволинейный интеграл I рода обладает следующими свойствами:
|
||||||
|
Пример 1
|
||||||
|
Найти интеграл
 вдоль отрезка прямой вдоль отрезка прямой Решение. 
|
||||||
|
Пример 2
|
||||||
|
Вычислить интеграл
 , где C − дуга окружности , где C − дуга окружности  . .
Решение.    |
||||||
|
Пример 3
|
||||||
|
Вычислить интеграл
 , где C − кривая, заданная уравнением , где C − кривая, заданная уравнением  . .
Решение.    |
||||||
|
Пример 4
|
||||||
|
Вычислить интеграл
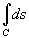 , где C является отрезком прямой от точки O(0,0) до A(1,2) (рисунок 4 выше). , где C является отрезком прямой от точки O(0,0) до A(1,2) (рисунок 4 выше).
Решение. 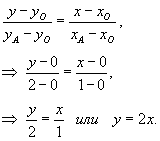 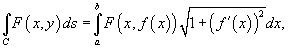 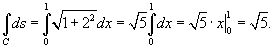 |
||||||
|
Пример 5
|
||||||
|
Вычислить интеграл
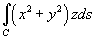 , где кривая C задана параметрически в виде , где кривая C задана параметрически в виде 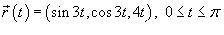 . .
Решение. 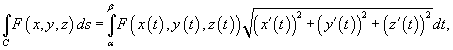 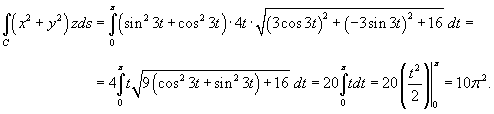 |
||||||
|
Пример 6
|
||||||
|
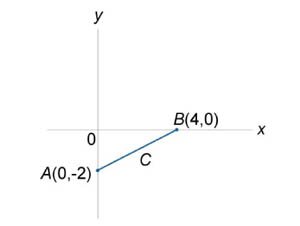
Вычислить криволинейный интеграл
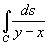 , где кривая C − отрезок прямой от точки (0,−2) до (4,0) , где кривая C − отрезок прямой от точки (0,−2) до (4,0) Решение. 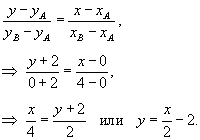 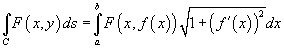 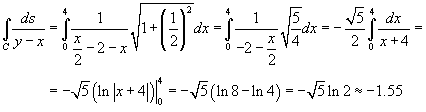
|
||||||
|
Пример 7
|
||||||
|
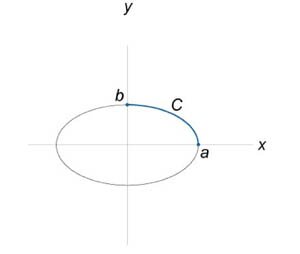
Найти криволинейный интеграл
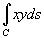 , где кривая C является дугой эллипса , где кривая C является дугой эллипса 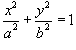 , лежащей в первом квадранте (рисунок 6). , лежащей в первом квадранте (рисунок 6).
Решение. 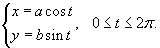 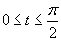 . Следовательно, по формуле . Следовательно, по формуле
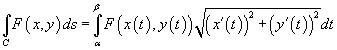 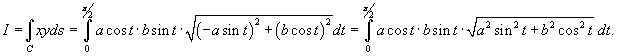 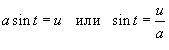 . Тогда . Тогда
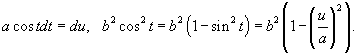 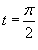 получаем получаем 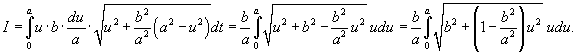 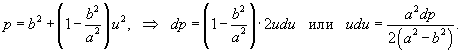 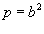 , и соответственно, если , и соответственно, если 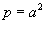 . Таким образом, . Таким образом,
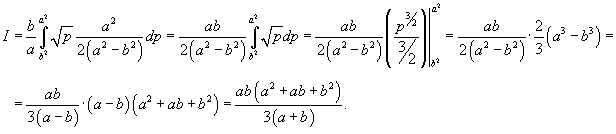 |
||||||



 и скалярная функция F непрерывна на кривой C, то
и скалярная функция F непрерывна на кривой C, то

 , то
, то

 , то
, то

 выражается формулой
выражается формулой

 .
.