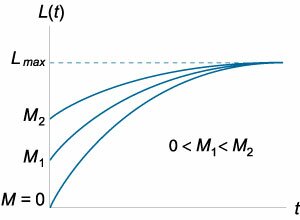
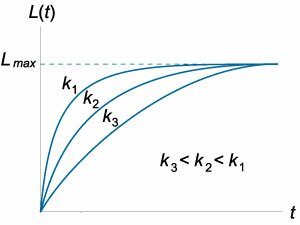
Кривая обучения

Освоение новой темы и приобретение новых навыков всегда требует времени. В данном разделе мы попробуем смоделировать процесс обучения, используя дифференциальные уравнения.

Прежде всего, введем некоторую измеряемую функцию обучения 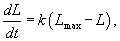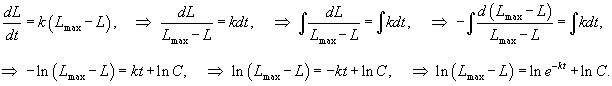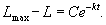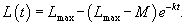L(t). Эта функция может описывать, например, текущую производительность труда работника. Пусть L_max будет являться максимально возможным значением L(t). Во многих случая справедливо следующее эмпирическое правило: скорость обучения пропорциональна объему оставшегося (еще невыученного) материала. Математически это представляется уравнением вида где k − коэффициент пропорциональности. Данное дифференциальное уравнение является уравнением с разделяющимися переменными, и его легко можно решить в общем виде: Избавляясь от логарифмов, получаем общее решение в форме: Постоянную C можно определить из начального условия: L(t = 0) = M. Следовательно, C = L_max − M. В результате кривая обучения описывается формулой В последнем выражении параметр M означает начальный уровень знаний или навыков. В простейшем случае можно предположить, что M = 0. Другой параметр k "контролирует" скорость обучения. Вид кривых обучения при различных значениях M и k показан на рисунках 1 и 2, соответственно. Как видно, кривая обучения L во всех случаях быстрее возрастает в начале процесса, а затем по мере снижения скорости обучения кривая приближается к максимальному значению L_max.

   Пример 1

Фармацевт в некоторой (скорее всего в английской) аптеке должен проверять 1,000 рецептов в день. Новый фармацевт после найма на работу через 1 неделю смог проверить 100 рецептов в день. Оценить число рецептов, которые фармацевт сможет проверить в течение дня еще через одну неделю. Для простоты положим начальный уровень навыка равным нулю: M = 0. Процесс обучения можно описать следующим законом: Определим параметр k, зная количество рецептов, которые проверяются через 1 неделю: Подставляя t = 1 неделя, находим: Теперь можно вычислить производительность нового фармацевта спустя две недели после начала работы:

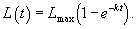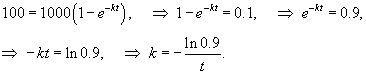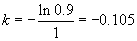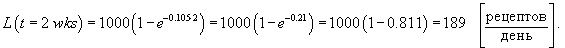   Пример 2

Предположим, что новость распространяется в средствах массовой информации по закону, описываемому кривой обучения. Каков должен быть первоначальный процент "популяции", осведомленных об этой новости, так чтобы через 1 неделю это уровень достигнул 50%, а через 4 недели − 90%? Новость распространяется по закону: Мы знаем две точки на этой кривой: в моменты времени t = 1 неделя и t = 4 недели. Поэтому, можно записать следующие два уравнения: Здесь параметр M представлен как rL_max, где r лежит в интервале 0 ≤ r ≤ 1, а время t выражено в неделях.

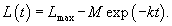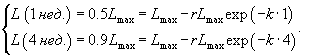Разделив на L_max, получаем систему уравнений с двумя неизвестными: r и k: 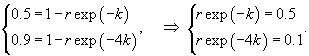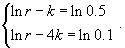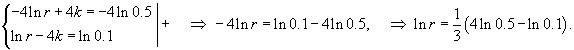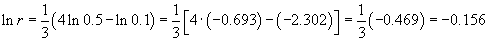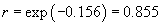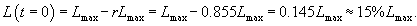Возьмем логарифмы от обеих частей каждого уравнения: Исключим параметр k из системы, умножая первое уравнение на (−4) и затем складывая оба уравнения: В результате простых вычислений получаем ответ: Отсюда следует, что параметр r равен Таким образом, в данном случае начальный уровень "проникновения" новости должен составлять