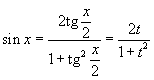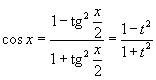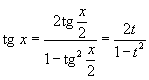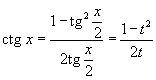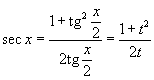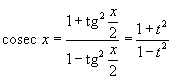|
Интегрирование рациональных выражений тригонометрических функций
|
||||||
|
Интегрирование любого рационального выражения тригонометрических функций можно всегда свести к интегрированию алгебраической рациональной функции используя универсальную тригонометрическую подстановку
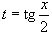 ). ).Для преобразования рациональных выражений от
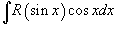 , где R - рациональная функция, используется подстановка , где R - рациональная функция, используется подстановка 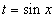 . .Аналогично, для вычисления интеграла вида 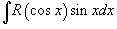 , где R - рациональная функция, используется подстановка , где R - рациональная функция, используется подстановка 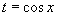 . .Если подынтегральное выражение является только функцией tg x, то подстановка Для вычисления интеграла вида 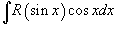 , где обе функции sin x и cos x входят в четной степени, применяется подстановка , где обе функции sin x и cos x входят в четной степени, применяется подстановка 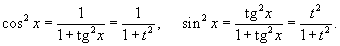 |
||||||
|
Пример 1
|
||||||
|
Вычислить интеграл
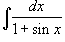 . .
Решение. 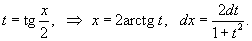 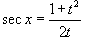 , получаем , получаем
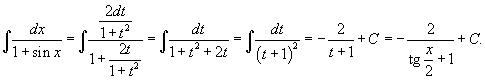 |
||||||
|
Пример 2
|
||||||
|
Вычислить интеграл
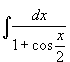 . .
Решение. 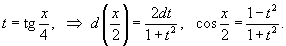 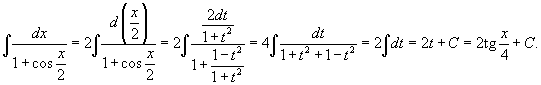 |
||||||
|
Пример 3
|
||||||
|
Вычислить интеграл
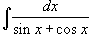 . .
Решение. 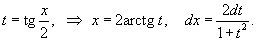 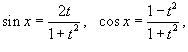 мы получаем мы получаем
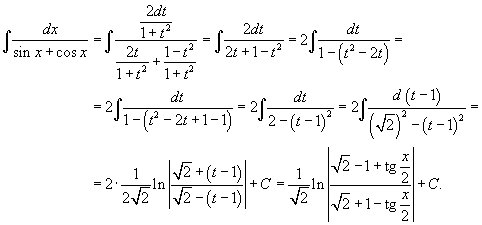 |
||||||
|
Пример 4
|
||||||
|
Вычислить интеграл
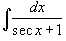 . .
Решение. 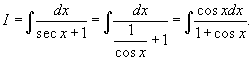 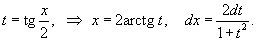 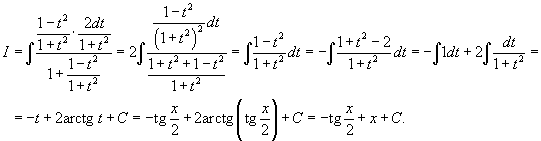 |
||||||
|
Пример 5
|
||||||
|
Вычислить интеграл
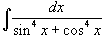 . .
Решение. 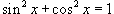 , мы можем записать , мы можем записать
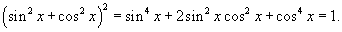 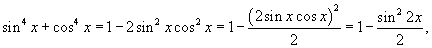 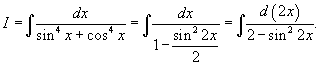 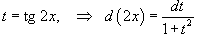 . Далее используем соотношение . Далее используем соотношение
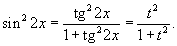 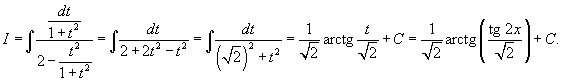 |
||||||
|
Пример 6
|
||||||
|
Вычислить интеграл
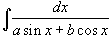 . .
Решение. 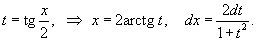 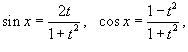 находим интеграл: находим интеграл:
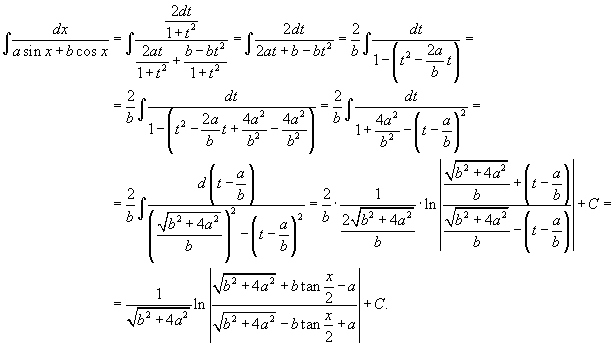 |
||||||
|
Пример 7
|
||||||
|
Найти интеграл
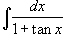 . .
Решение. 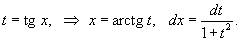 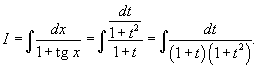 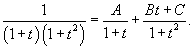 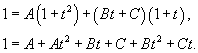 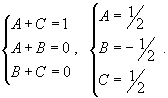 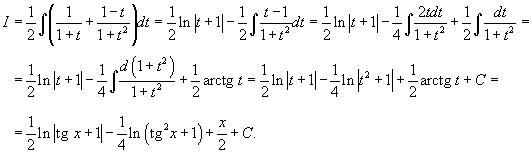 |
||||||