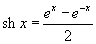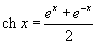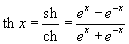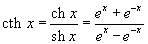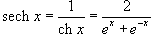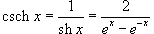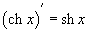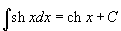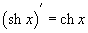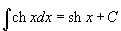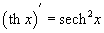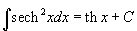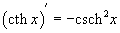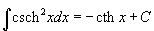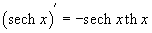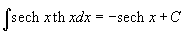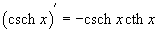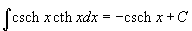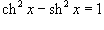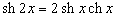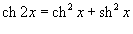|
Интегрирование гиперболических функций
|
||||||||||||||||||
|
Шесть основных гиперболических функций определяются следующим образом:
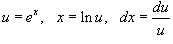 . . |
||||||||||||||||||
|
Пример 1
|
||||||||||||||||||
|
Вычислить интеграл
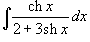 . .
Решение. 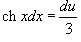 . Следовательно, интеграл равен . Следовательно, интеграл равен
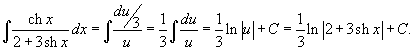 |
||||||||||||||||||
|
Пример 2
|
||||||||||||||||||
|
Вычислить интеграл
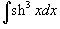 . .
Решение. 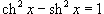 , и, следовательно, , и, следовательно, 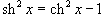 , интеграл можно переписать в виде , интеграл можно переписать в виде
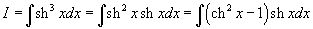 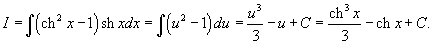 |
||||||||||||||||||
|
Пример 3
|
||||||||||||||||||
|
Вычислить
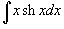 . .
Решение. 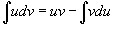 . Пусть . Пусть 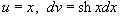 . Тогда . Тогда 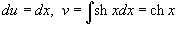 . В результате находим интеграл . В результате находим интеграл
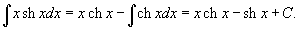 |
||||||||||||||||||
|
Пример 4
|
||||||||||||||||||
|
Вычислить интеграл
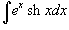 . .
Решение. 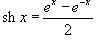 , то интеграл равен , то интеграл равен
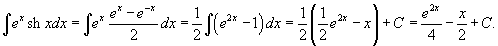 |
||||||||||||||||||
|
Пример 5
|
||||||||||||||||||
|
Найти интеграл
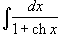 . .
Решение. 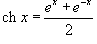 . Подставляя это в интеграл, получаем . Подставляя это в интеграл, получаем
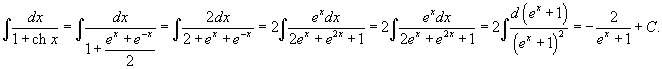 |
||||||||||||||||||
|
Пример 6
|
||||||||||||||||||
|
Найти интеграл
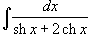 . .
Решение. 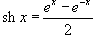 и и 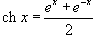 . Следовательно, . Следовательно,
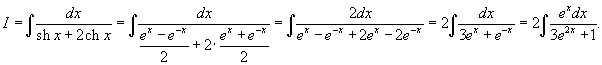 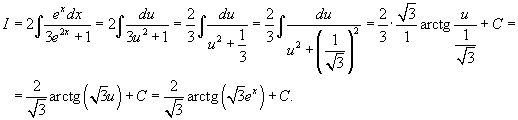 |
||||||||||||||||||
|
Пример 7
|
||||||||||||||||||
|
Вычислить интеграл
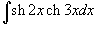 . .
Решение. 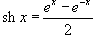 и и 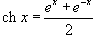 , получаем , получаем
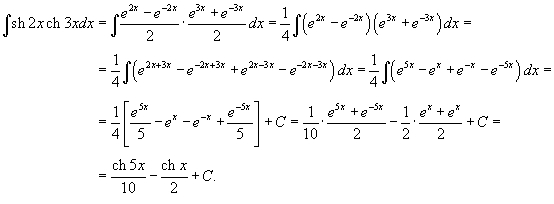 |
||||||||||||||||||
|
Пример 8
|
||||||||||||||||||
|
Вычислить интеграл
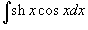 . .
Решение. 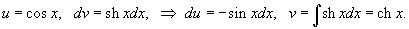 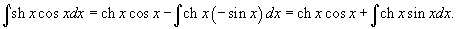 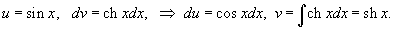 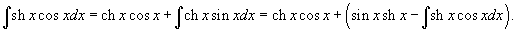 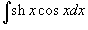 , находим ответ , находим ответ
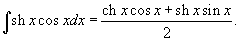 |
||||||||||||||||||