|
Интегральный признак Коши
|
|
Пусть
  , и расходится, если , и расходится, если  . . |
|
Пример 1
|
|
Определить, сходится или расходится ряд
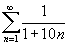 . .
Решение.
Используем интегральный признак Коши. Вычислим соответствующий несобственный интеграл:
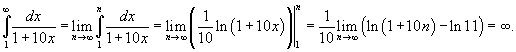 |
|
Пример 2
|
|
Показать, что обобщенный гармонический ряд
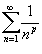 сходится при сходится при
Решение.
Рассмотрим соответствующую функцию 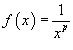 и применим интегральный признак. Несобственный интеграл равен и применим интегральный признак. Несобственный интеграл равен
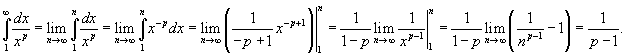 |
|
Пример 3
|
|
Определить, сходится или расходится ряд
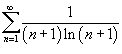 . .
Решение.
Вычислим соответствующий несобственный интеграл:
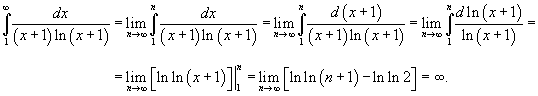 |
|
Пример 4
|
|
Исследовать ряд
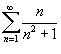 на сходимость. на сходимость.
Решение.
Оценим несобственный интеграл
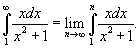 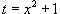 . Тогда . Тогда 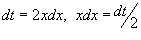 . Находим значение интеграла: . Находим значение интеграла:
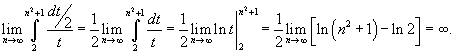 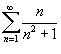 также расходится. также расходится. |
|
Пример 5
|
|
Исследовать ряд
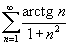 на сходимость. на сходимость.
Решение.
Заметим, что 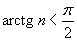 . Тогда по признаку сравнения получаем . Тогда по признаку сравнения получаем
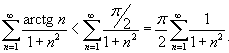 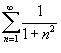 : :
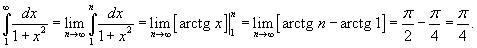 |
|
Пример 6
|
|
Определить, сходится или расходится ряд
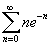 . .
Решение.
Применяя интегральный признак, вычислим соответствующий несобственный интеграл:
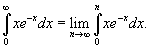 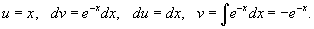 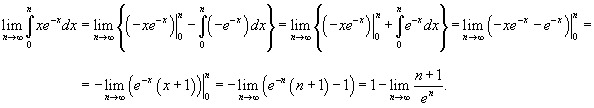 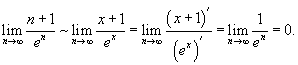 |