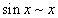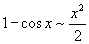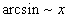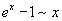|
Бесконечно малые функции
|
||||||||||
|
Функция
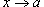 , если , если
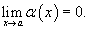 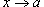 . .
|
||||||||||
|
Пример 1
|
||||||||||
|
Найти предел
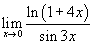 . .
Решение. 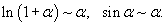 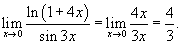 |
||||||||||
|
Пример 2
|
||||||||||
|
Найти предел
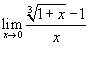 . .
Решение. 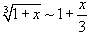 , то предел можно переписать в следующем виде: , то предел можно переписать в следующем виде:
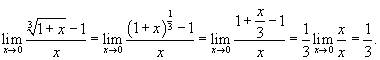 |
||||||||||
|
Пример 3
|
||||||||||
|
Найти предел
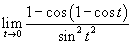 . .
Решение. 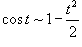 и и 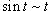 при при 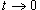 . Следовательно, . Следовательно,
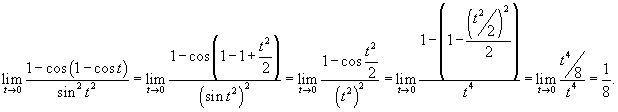 |
||||||||||
|
Пример 4
|
||||||||||
|
Найти предел
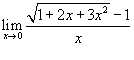 . .
Решение. 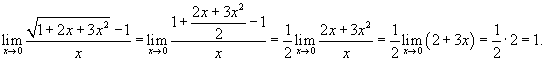 |
||||||||||
|
Пример 5
|
||||||||||
|
Найти предел
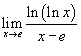 . .
Решение. 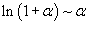 при при 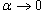 . В результате предел преобразуется следующим образом: . В результате предел преобразуется следующим образом:
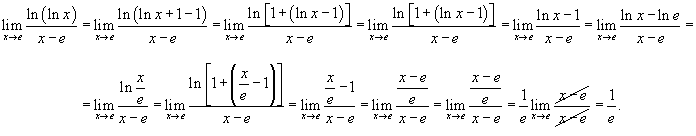 |
||||||||||
|
Пример 6
|
||||||||||
|
Вычислить предел
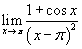 . .
Решение. 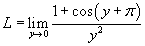 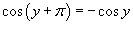 , получаем , получаем
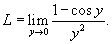 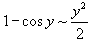 , находим предел: , находим предел:
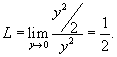 |
||||||||||
|
Пример 7
|
||||||||||
|
Вычислить предел
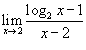 . .
Решение. 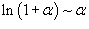 при при 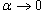 , получаем , получаем
 |
||||||||||
|
Пример 8
|
||||||||||
|
Вычислить предел
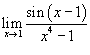 . .
Решение. 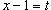 . Тогда . Тогда 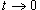 при при 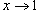 . Предел становится равным . Предел становится равным
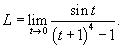 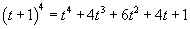 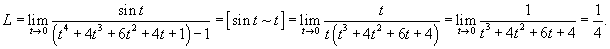 |
||||||||||
|
Пример 9
|
||||||||||
|
Вычислить предел
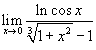 . .
Решение. 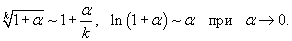 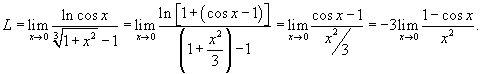 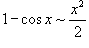 , получаем окончательный ответ , получаем окончательный ответ
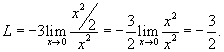 |
||||||||||
|
Пример 10
|
||||||||||
|
Вычислить предел
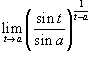 . .
Решение. 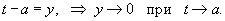 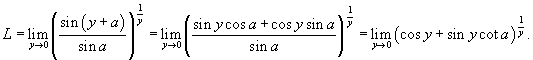 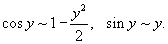 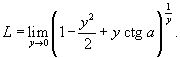 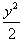 . В результате, получаем окончательный ответ . В результате, получаем окончательный ответ
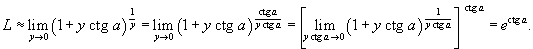 |
||||||||||
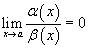 , то говорят, что функция
, то говорят, что функция 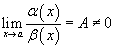 , то говорят, что функции
, то говорят, что функции 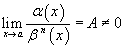 , то говорят, что функция
, то говорят, что функция 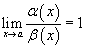 , то говорят, что бесконечно малые функции
, то говорят, что бесконечно малые функции