|
Бесконечные последовательности
|
|
Функция
Множество значений Числовая последовательность 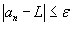 . В этом случае мы записываем . В этом случае мы записываем
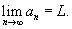 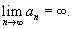 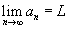 существует и L конечно, то говорят, что числовая последовательность сходится. существует и L конечно, то говорят, что числовая последовательность сходится.В противном случае последовательность расходится. Теорема "о двух милиционерах": Предположим, что 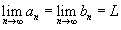 и и 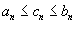 для всех для всех 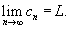 Если числовая последовательность сходится, то она ограничена. Любая неограниченная последовательность расходится. Последовательность |
|
Пример 1
|
|
Записать общую формулу для n-го члена
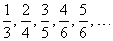 Решение. 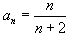 . Тогда предел равен . Тогда предел равен
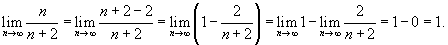 |
|
Пример 2
|
|
Записать формулу n-го члена
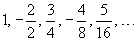 Решение. 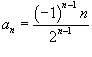 . Поскольку . Поскольку 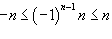 , то можно записать , то можно записать
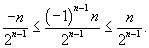 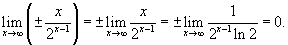 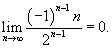 |
|
Пример 3
|
|
Определить, сходится или расходится последовательность
 ? ?
Решение. 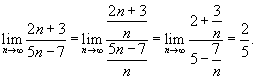 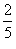 . . |
|
Пример 4
|
|
Определить, сходится или расходится последовательность
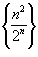 ? ?
Решение. 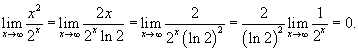 |
|
Пример 5
|
|
Определить, является ли последовательность
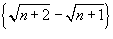 сходящейся или расходящейся? сходящейся или расходящейся?
Решение. 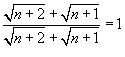 . В результате получаем . В результате получаем
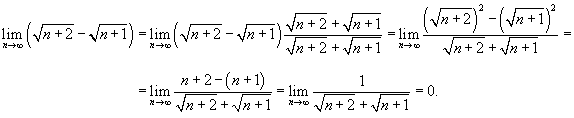 |
|
Пример 6
|
|
Определить, является ли последовательность
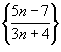 монотонно возрастающей, убывающей или немонотонной? монотонно возрастающей, убывающей или немонотонной?
Решение. 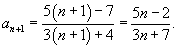 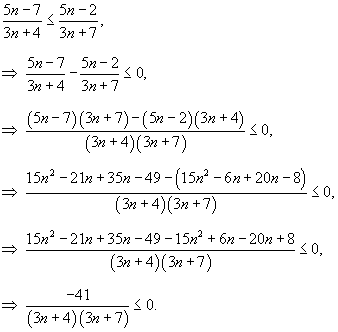 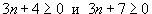 при при |
|
Пример 7
|
|
Исследовать числовую последовательность
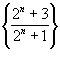 на монотонность. на монотонность.
Решение. 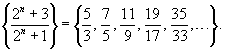 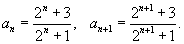 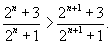 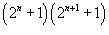 : :
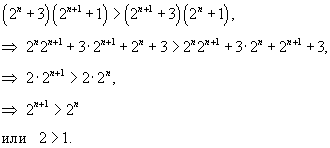 |