Неравенства и промежутки числовой прямой

Неравенство	Промежуток	Графическое обозначение
a ≤ x ≤ b	[a, b]
a < x ≤ b	(a, b]
a ≤ x < b	[a, b)
a < x < b	(a, b)
− ∞ < x ≤ b  или  x ≤ b	(− ∞, b]
− ∞ < x < b  или  x < b	(− ∞, b)
a ≤ x < ∞  или  x ≥ a	[a, ∞)
a < x < ∞  или  x > a	(a, ∞)

Строгие неравенства
a < b означает "a меньше, чем b",
a > b означает "a больше, чем b".

Нестрогие неравенства
a ≤ b означает "a меньше или равно b",
a ≥ b означает "a больше или равно b".

Если a > b, то b < a.

Если a > b, то a − b > 0 или (эквивалентно) b − a < 0.

Свойство транзитивности
Если a > b и b > c, то a > c.

Знак неравенства сохраняется, если к обеим частям прибавить одно и то же произвольное число:
Если a > b, то a + c > b + c.

Любое слагаемое можно перенести из одной части неравенства в другую, изменив его знак на противоположный:
Если a + b > c, то a > c − b.

Если a > b и c > d, то a + c > b + d.

Если a > b и c > d, то a − d > b − c.

Знак неравенства сохраняется, если обе части умножить на одно и то же положительное число:
Если a > b и m > 0, то ma > mb.

Знак неравенства сохраняется, если обе части разделить на одно и то же положительное число:
Если a > b и m > 0, то a/m > b/m.

Знак неравенства меняется на противоположный, если обе части умножить на одно и то же отрицательное число:
Если a > b и m < 0, то ma < mb.

Знак неравенства меняется на противоположный, если обе части разделить на одно и то же отрицательное число:
Если a > b и m < 0, то a/m < b/m.

Если a > b > 0, то 1/b > 1/a.

Умножение неравенств
Если a > b > 0 и c > d > 0, то ac > bd.

Деление неравенств
Если a ≥ b > 0 и c > d > 0, то a/d > b/c.

Возведение неравенства в степень при положительном показателе
Если a > b > 0 и n > 0, то aⁿ > bⁿ.

Возведение неравенства в степень при отрицательном показателе
Если a > b > 0 и n < 0, то aⁿ < bⁿ.

Извлечение корня из неравенства
Если a > b > 0, то .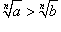

Равенство имеет место лишь при a = 1.

Неравенство Коши (соотношение между средним арифметическим и средним геометрическим)
√ab  ≤ (a + b)/2,  где a > 0, b > 0.
Равенство выполняется лишь при a = b.

Неравенство Коши (случай нескольких переменных)

Линейное неравенство (случай a > 0)
Если ax + b > 0 и a > 0, то x > − b/a.

Линейное неравенство (случай a < 0)
Если ax + b > 0 и a < 0, то x < − b/a.

Квадратное неравенство
ax² + bx + c > 0

	a > 0	a < 0
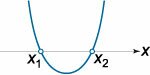
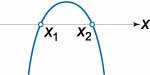
D > 0	x < x1, x > x2	x1 < x < x2
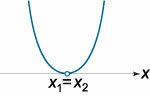
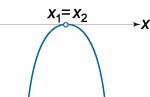
D = 0	x < x1, x > x1	x ∈ ∅
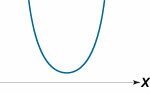
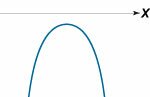
D < 0	− ∞ < x < ∞	x ∈ ∅

|a + b| ≤ |a| + |b|

Если |x| < a, то −a < x < a,  где a > 0.

Если |x| > a, то x < −a  и  x > a,  где a > 0.

Если x² < a, то |x| < √a  ,  где a > 0.

Если x² > a, то |x| > √a  ,  где a > 0.