|
Неопределенный интеграл и его свойства. Таблица интегралов.
|
||||||||||||||||||||||||||||||||
|
Определение первообразной и неопределенного интеграла
Функция 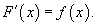  
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,а, k, C - постоянные величины.
Таблица интегралов
В формулах ниже предполагается, что
|
||||||||||||||||||||||||||||||||
|
Пример 1
|
||||||||||||||||||||||||||||||||
|
Вычислить
 . .
Решение.  |
||||||||||||||||||||||||||||||||
|
Пример 2
|
||||||||||||||||||||||||||||||||
|
Вычислить интеграл
 . .
Решение.  |
||||||||||||||||||||||||||||||||
|
Пример 3
|
||||||||||||||||||||||||||||||||
|
Вычислить
 . .
Решение.  . Тогда . Тогда
 |
||||||||||||||||||||||||||||||||
|
Пример 4
|
||||||||||||||||||||||||||||||||
|
Вычислить
 . .
Решение.  , находим , находим
 |
||||||||||||||||||||||||||||||||
|
Пример 5
|
||||||||||||||||||||||||||||||||
|
Вычислить
 . .
Решение.  , интеграл равен , интеграл равен
 |
||||||||||||||||||||||||||||||||
|
Пример 6
|
||||||||||||||||||||||||||||||||
|
Вычислить интеграл
 без использования замены переменной. без использования замены переменной.
Решение.  |
||||||||||||||||||||||||||||||||



































