|
Несобственные интегралы
|
||||||
|
Определенный интеграл
 называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий: называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:
Бесконечные пределы интегрирования
Пусть   В противном случае интегралы расходятся. Пусть   также сходится; в противном случае он расходится. также сходится; в противном случае он расходится.
Теоремы сравнения
Пусть 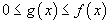 для всех x в интервале для всех x в интервале
Интеграл от разрывной функции
Пусть функция   Пусть  . Тогда справедливо соотношение . Тогда справедливо соотношение
  сходится, если оба интеграла в правой части верхнего равенства сходятся. В противном случае несобственный интеграл расходится. сходится, если оба интеграла в правой части верхнего равенства сходятся. В противном случае несобственный интеграл расходится. |
||||||
|
Пример 1
|
||||||
|
Определить, при каких значениях k интеграл
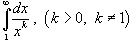 сходится. сходится.
Решение. 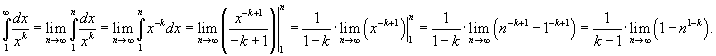
|
||||||
|
Пример 2
|
||||||
|
Вычислить интеграл
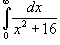 . .
Решение. 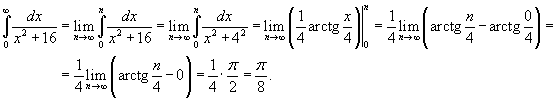 |
||||||
|
Пример 3
|
||||||
|
Определить, сходится или расходится несобственный интеграл
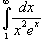 ? ?
Решение.  для всех для всех 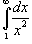 сходится (смотрите пример 1), то искомый интеграл сходится (смотрите пример 1), то искомый интеграл 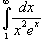 также сходится по теореме сравнения 1. также сходится по теореме сравнения 1. |
||||||
|
Пример 4
|
||||||
|
Вычислить интеграл
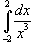 . .
Решение. 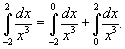 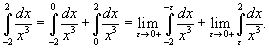 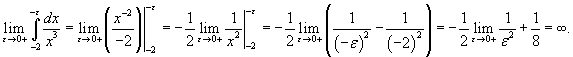 |
||||||
|
Пример 5
|
||||||
|
Определить, сходится или расходится несобственный интеграл
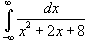 ? ?
Решение. 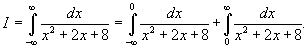 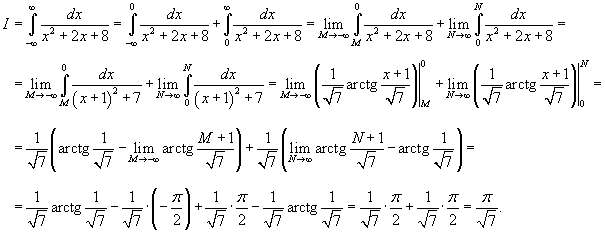 |
||||||
|
Пример 6
|
||||||
|
Определить, сходится или расходится несобственный интеграл
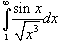 ? ?
Решение. 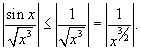 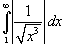 сходится (смотрите также пример 1). Действительно, сходится (смотрите также пример 1). Действительно,
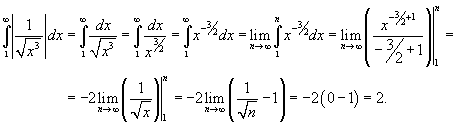  сходится по теореме сравнения 1. Тогда искомый интеграл сходится по теореме сравнения 1. Тогда искомый интеграл 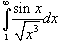 также сходится (причем абсолютно) по теореме сравнения 3. также сходится (причем абсолютно) по теореме сравнения 3. |
||||||
|
Пример 7
|
||||||
|
Определить, сходится или расходится несобственный интеграл
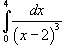 ? ?
Решение. 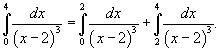 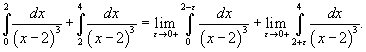 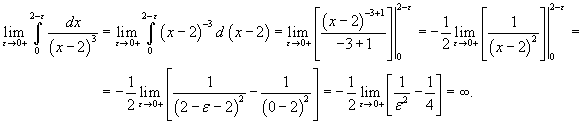 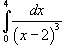 также расходится. также расходится. |
||||||
|
Пример 8
|
||||||
|
Определить, при каких значениях k интеграл
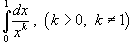 сходится. сходится.
Решение. 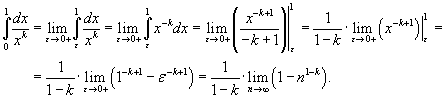
|
||||||
|
Пример 9
|
||||||
|
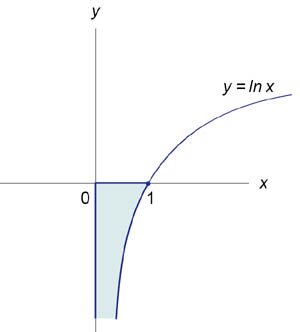
Найти площадь под кривой
Решение.  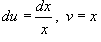 . Следовательно, . Следовательно,
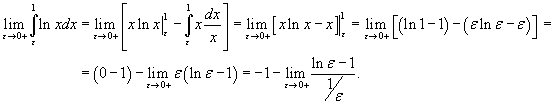 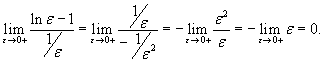 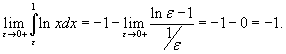 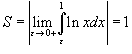 . .
|
||||||
|
Пример 10
|
||||||
|
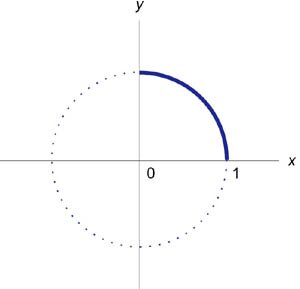
Вычислить периметр единичной окружности.
Решение. Уравнение единичной окружности с центром в начале координат имеет вид 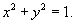 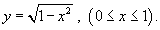 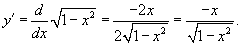 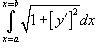 . Следовательно, . Следовательно,
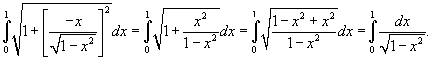  . .
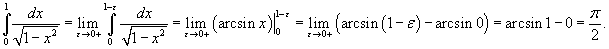 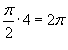 . .
|
||||||
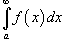 сходится, то
сходится, то 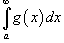 также сходится;
также сходится; сходится, то
сходится, то 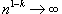 при
при 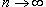 и интеграл расходится;
и интеграл расходится;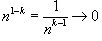 при
при 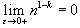 и интеграл сходится;
и интеграл сходится;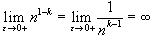 и интеграл расходится.
и интеграл расходится.